题目内容
【题目】=如图,在半径为2的⊙O中,弦AB=2,⊙O上存在点C,使得弦AC=2 ![]() ,则∠BOC=°.
,则∠BOC=°. 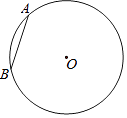
【答案】150°或30°
【解析】解:如图1,作OD⊥AB于D,OE⊥AC于E,连结OA,OA=2,如图, 
∴AD=BD= ![]() AB=1,AE=CE=
AB=1,AE=CE= ![]() AC=
AC= ![]() ,
,
在Rt△OAE中,OE= ![]() ,
,
∴∠EAO=45°,
在Rt△OAD中,OD= ![]() =
= ![]() ,
,
∴∠DAO=60°,
∴∠BAC=45°+60°=105°,
∴∠BOC=150°,
如图2,
同理:∠BAC=60°﹣45°=15°,
∴∠BOC=30°,
所以答案是150°或30°.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目