��Ŀ����
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�ֱ��AB��y=��x+b��y���ڵ�A��0��4������x���ڵ�B��
��1����ֱ��AB�ı���ʽ�͵�B�����ꣻ
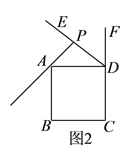
��2��ֱ��l��ֱƽ��OB��AB�ڵ�D����x���ڵ�E����P��ֱ��l��һ���㣬���ڵ�D���Ϸ������P��������Ϊn��
���ú�n�Ĵ���ʽ��ʾ��ABP�������
�ڵ�S��ABP=8ʱ�����P�����ꣻ
���ڢڵ������£���PBΪб���ڵ�һ����������ֱ����PBC�����C�����꣮
���𰸡���1��AB:y=-x+4��B(4��0)����2����S��ABP=2n-4����P(2��6)����C(6��4).
�����������������
��1���ѵ�A��0��4������y=��x+b���b��ֵ�����ɵõ�һ�κ����Ľ���ʽ���ɽ���ʽ������õ�B�����ꣻ
��2��������1���������B������Ϊ��4��0����������֪��ֱ��PEΪ�� ![]() ���ɴ˿���õ�D�����꣬�Ӷ����ú���n���Ĵ���ʽ�����PD�ij�����S��ABP=
���ɴ˿���õ�D�����꣬�Ӷ����ú���n���Ĵ���ʽ�����PD�ij�����S��ABP=![]() PD��OB�����ú���n������������
PD��OB�����ú���n������������
����S��ABP=8������������ı���ʽ�����ⷽ�̼��������n����ֵ���Ӷ��ɵô�ʱ��P�����ꣻ
������ͼ�����C1��C2�Ƿ�������ĵ�C�����������ã��ı���BC1PC2�������Σ�����C1��C1M��x���ڵ�M������P��PN����MC1�ڵ�N�����ı���PEMN�Ǿ��Σ���C1MB�ա�PNC1����BM= ![]() ����C1M=MN-NC1=
����C1M=MN-NC1= ![]() ����Rt��PBE�У��ɹ��ɶ�������ã�PB=
����Rt��PBE�У��ɹ��ɶ�������ã�PB=![]() ������Rt��BMC1�У���BM2+C1M2=BC12���������ڡ�
������Rt��BMC1�У���BM2+C1M2=BC12���������ڡ�![]() ���ַ��̣��ⷽ����á�
���ַ��̣��ⷽ����á�![]() ����ֵ��������õ�C1�����ꣻͬ������õ�C2�����ꣻ����ϵ�C�ڵ�һ������һ�������ɵõ���C������.
����ֵ��������õ�C1�����ꣻͬ������õ�C2�����ꣻ����ϵ�C�ڵ�һ������һ�������ɵõ���C������.
���������
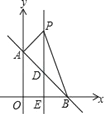
��1����ֱ��AB��y=��x+b��y���ڵ�A��0��4����
��b=4��
��ֱ��AB�ı���ʽΪ��y=��x+4.
����y=��x+4������y=0ʱ��x=4��
��ֱ��AB��x��Ľ���B������Ϊ��4��0����
��2���١���B������Ϊ��4��0����
��OB=4��
��ֱ��l��ֱƽ��OB��AB�ڵ�D����x���ڵ�E��
����D�ĺ�����Ϊ2��
����y=-x+4������x=2ʱ��y=-2+4=2��
����D��������2��2��.
��P��ֱ��l��һ���㣬���ڵ�D���Ϸ�����P��������Ϊn��
��PD=n-2��
��S��ABP=![]() PD��OB=
PD��OB=![]() ��
��
����S��ABP=8ʱ����![]() �����
����� ![]() ��
��
����ʱ��P������Ϊ��2��6����
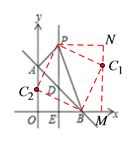
����ͼ�����C1��C2�Ƿ�������ĵ�C�����������ã��ı���BC1PC2�������Σ�����C1��C1M��x���ڵ�M������P��PN����MC1�ڵ�N�����ı���PEMN�Ǿ��Σ���C1MB�ա�PNC1��
��MN=PE=6��NC1=BM��PN=C1M=BM+BE��
��BM= ![]() ����C1M=MN-NC1=
����C1M=MN-NC1= ![]() .
.
����Rt��PBE��PE=6��BE=![]() OB=2��
OB=2��
��PB=![]() ��
��
����PB�ǵ���Rt��PC1B��б����
��BC1=![]() .
.
����Rt��BMC1��BM2+C1M2=BC12��
��![]() �������
������� ![]() ��
��
����![]() ʱ��PN=C1M=6-4=2<BM+BE��
ʱ��PN=C1M=6-4=2<BM+BE��
��![]() ֻ��ȡ2��
ֻ��ȡ2��
��BM=2��C1M=6-2=4��
��OM=OB+BM=4+2=6��
����C1��������6��4����
ͬ������õ�C2������Ϊ��0��2����
������C�ڵ�һ���ޣ�
����C��������6��4��.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�