题目内容
【题目】数学兴趣小组在“用面积验证平方差公式”时,经历了如下的探究过程;
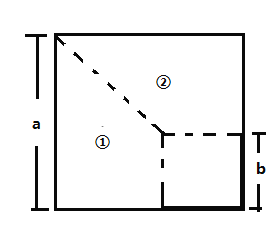
(1)小明的想法是:将边长为![]() 的正方形右下角剪掉一个边长为
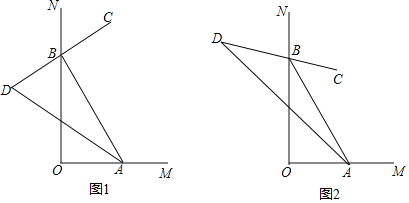
的正方形右下角剪掉一个边长为![]() 的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,并用两种方式表示这两部分面积的和,请你按照小明的想法验证平方差公式.
的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,并用两种方式表示这两部分面积的和,请你按照小明的想法验证平方差公式.
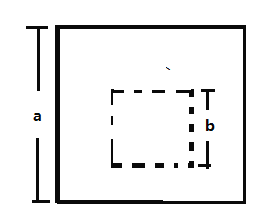
(2)小白的想法是:在边长为![]() 的正方形内部任意位置剪掉一个边长为
的正方形内部任意位置剪掉一个边长为![]() 的正方形(如图2),再将剩下部分进行适当分割,并将分割得到的几部分面积和用两种方式表示出来,请你按照小白的想法在图中用虚线画出分割线,并验证平方差公式.
的正方形(如图2),再将剩下部分进行适当分割,并将分割得到的几部分面积和用两种方式表示出来,请你按照小白的想法在图中用虚线画出分割线,并验证平方差公式.
【答案】(1)证明见解析;(2)见解析.
【解析】
(1)先根据方式一:①![]() ②的面积等于两个正方形的面积之差;方式二:①
②的面积等于两个正方形的面积之差;方式二:①![]() ②的面积等于两个直角梯形的面积之和;然后根据方式一和方式二计算的面积相等即可验证平方差公式;
②的面积等于两个直角梯形的面积之和;然后根据方式一和方式二计算的面积相等即可验证平方差公式;
(2)如图(见解析),先根据方式一:①![]() ②
②![]() ③
③![]() ④的面积等于两个正方形的面积之差;方式二:①
④的面积等于两个正方形的面积之差;方式二:①![]() ②
②![]() ③
③![]() ④的面积等于四个长方形的面积之和,然后根据方式一和方式二计算的面积相等即可验证平方差公式.
④的面积等于四个长方形的面积之和,然后根据方式一和方式二计算的面积相等即可验证平方差公式.
(1)方式一:①![]() ②的面积等于两个正方形的面积之差
②的面积等于两个正方形的面积之差
则①![]() ②的面积为
②的面积为![]()
方式二:①![]() ②的面积等于两个直角梯形的面积之和
②的面积等于两个直角梯形的面积之和
则①![]() ②的面积为
②的面积为![]()
由方式一和方式二的面积相等可得:![]() ;
;
(2)如图,方式一:①![]() ②
②![]() ③
③![]() ④的面积等于两个正方形的面积之差
④的面积等于两个正方形的面积之差
则①![]() ②
②![]() ③
③![]() ④的面积为
④的面积为![]()
方式二:①![]() ②
②![]() ③
③![]() ④的面积等于四个长方形的面积之和
④的面积等于四个长方形的面积之和
①![]() ②的面积为
②的面积为![]()
③![]() ④的面积为
④的面积为![]()
则①![]() ②
②![]() ③
③![]() ④的面积为
④的面积为![]()
由方式一和方式二的面积相等可得:![]() .
.


练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目