题目内容
3. 如图,直线y=-x+m与y=nx+3n(n≠0)的交点的横坐标为-1,则关于x的不等式-x+m>nx+3n>0的整数解为( )
如图,直线y=-x+m与y=nx+3n(n≠0)的交点的横坐标为-1,则关于x的不等式-x+m>nx+3n>0的整数解为( )| A. | -1 | B. | -5 | C. | -4 | D. | -2 |
分析 满足不等式-x+m>nx+3n>0就是直线y=-x+m位于直线y=nx+3n的上方且位于x轴的上方的图象,据此求得自变量的取值范围即可.
解答 解:∵直线y=-x+m与y=nx+3n的交点的横坐标为-1,
∴关于x的不等式-x+m>nx+3n的解集为x<-1,
∵y=x+3=0时,x=-3,
∴nx+3n>0的解集是x>-3,
∴-x+m>nx+3n>0的解集是-3<x<-1,
所以不等式-x+m>nx+3n>0的整数解为-2,
故选:D
点评 本题考查了一次函数的图象和性质以及与一元一次不等式的关系,关键是根据不等式-x+m>nx+3n>0就是直线y=-x+m位于直线y=nx+3n的上方且位于x轴的上方的图象来分析.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
13. 在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )
在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )
 在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )
在数轴上标注了四段范围,如图所示,则表示-$\sqrt{10}$的点落在( )| A. | 段① | B. | 段② | C. | 段③ | D. | 段④ |
11.月亮超市正在热销某种商品,其标价为每件10元,若这种商品打7折销售,则每件可获利1元,设该商品每件的进价为x元,根据题意可列出的一元一次方程为( )
| A. | 10×0.7-x=1 | B. | 10-x×0.7=1 | C. | (10-x)×0.7=1 | D. | 10-x=1×0.7 |
15.实数$\sqrt{2}$,-3.14,0,$\sqrt{16}$中,无理数共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 在菱形ABCD中,对角线AC,BD交于点O,E为AC上点,且CE=CB,F为BE上点,M为BC上点,且MF⊥BE,并与OB相交于点N.
在菱形ABCD中,对角线AC,BD交于点O,E为AC上点,且CE=CB,F为BE上点,M为BC上点,且MF⊥BE,并与OB相交于点N. 如图,△ABC向右平移得到△DEF,若∠B=50°,∠D=60°,则∠F=70°.
如图,△ABC向右平移得到△DEF,若∠B=50°,∠D=60°,则∠F=70°.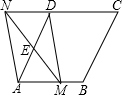 如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.