Question

【题目】如图，在平面直角坐标系中，点的坐标为（1,0），点的横坐标为2，将点 绕点P旋转，使它的对应点恰好落在轴上（不与点重合）；再将点绕点O逆时针旋转90°得到点.

(1)直接写出点和点C的坐标；

(2)求经过A，B,C三点的抛物线的表达式.

Answer 1

【答案】（1）点B的坐标为（3,0），点C的坐标为（0，3）；（2）.

【解析】试题分析：（1）过P作PM⊥x轴于点M，由AM=BM，可得B点坐标，由点绕点O逆时针旋转90°得到点C，可得点C坐标；

（2）这出抛物线解析式的一般形式，代入A、B、C三点坐标即可求得a、b、c的值，由此可得抛物线的解析式.

（1）如图：

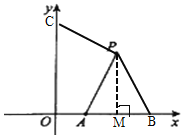
过P作PM⊥x轴于点M，则M（2，0），

∵PA=PB，A（1，0），

∴AM=BM，

∴B（3，0），

∵OB=OC，

∴C（0，3）.

故：点B的坐标为（3，0），点C的坐标为（0，3）；

（2）设抛物线的解析式为.因为 它经过A（1，0）， B（3，0）， C（0，3），

则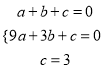，解得，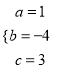

∴经过A，B，C三点的抛物线的表达式为.