题目内容
10.某中学对全校九年级男生进行了立定跳远项目测试,并从参加测试的500名男生中随机抽取了部分男生的测试成绩(单位:米)作为样本进行分析,绘制了如图所示的频数分布直方图.已知图中从左到右每个小长方形的高的比依次为3:5:7:6:4,其中1.80~2.00这-小组的频数为10,请根据有关信息解答下列问题:(1)填空:这次调查的样本容量为50,2.40~2.60这-小组的频数为8
(2)补全频数分布直方图;
(3)样本中男生立定跳远的人均成绩不低于多少米?
(4)请估计该校九年级男生立定跳远成绩在2.00米以上(包括2.00米)的约有多少人?
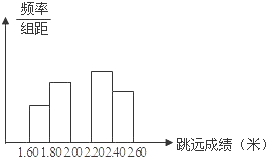
分析 (1)每小组的频率=小组的频数÷总人数.第2小组的频数为10;当组距相等时,长方形的高的比也就是频率比,这5个小组频率之比为3:5:7:6:4,可求得第2组频率为0.2;即可求得样本容量即总人数,用总人数乘以第2小组的频率可得2.40~2.60这-小组的频数;
(2)根据图中从左到右每个小长方形的高的比依次为3:5:7:6:4即可补全统计图;
(3)将各小组取最低成绩,利用加权平均数的计算公式即可得到结果;
(4)首先确定样本中立定跳远成绩在2.00米以上(包括2.00米)的频率,然后利用样本估计总体的思想即可估计该校九年级男生立定跳远成绩在2.00米以上(包括2.00米)的约有多少人.
解答 解:(1)样本容量=(3+5+7+6+4)÷5×10=50;
2.40~2.60这-小组的频数为:50×$\frac{4}{3+5+7+6+4}$=8.
故答案为50,8;
(2)如图: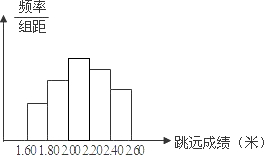
(3)设样本人均成绩最低值为$\overline{x}$,
∵各小组的频数分别为:$\frac{3}{25}$×50=6,$\frac{5}{25}$×50=10,$\frac{7}{25}$×50=14,$\frac{6}{25}$×50=12,$\frac{4}{25}$×50=8,
∴$\overline{x}$=$\frac{1}{50}$(1.60×6+1.80×10+2.00×14+2.20×12+2.40×8)=2.024,
∴样本中男生立定跳远的人均成绩不低于2.024米;
(4)估计该校九年级男生立定跳远成绩在2.00米以上(包括2.00米)的约有$\frac{14+12+8}{50}$×100%×500=340(人).
所以该校初三男生立定跳远成绩在2.00米以上的约有340人.
点评 本题考查读了直方图和频率的求法.解本题要懂得频率分布直分图的意义.也考查了平均数以及用样本估计总体.

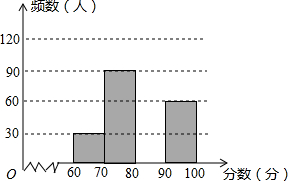 为了解某年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:
为了解某年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
(1)本次调查的样本容量为300;
(2)在表中:m=120,n=0.3;
(3)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在80≤x<90分数段内;
(4)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是60%.
其中正确的判断有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
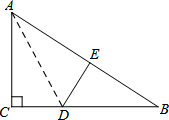 如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.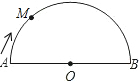 如图,在半圆O上有一动点M,点M从点A出发,沿弧AB、线段BA匀速运动回点A,设OM的长度为y,点M运动的时间为t,则y与t之间的函数图象大致为( )
如图,在半圆O上有一动点M,点M从点A出发,沿弧AB、线段BA匀速运动回点A,设OM的长度为y,点M运动的时间为t,则y与t之间的函数图象大致为( )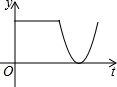
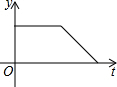


 如图,在平面直角坐标系xOy,直线y=x+1与y=-2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.
如图,在平面直角坐标系xOy,直线y=x+1与y=-2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.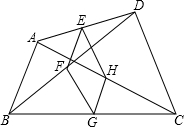 如图,四边形ABCD中,E、F、G、H分别为AD、BD、BC、AC的中点,顺次连结点E、F、G、H,所得四边形是一个怎样的四边形?请说明理由;若四边形EFGH是一个菱形,则四边形ABCD应满足什么条件?
如图,四边形ABCD中,E、F、G、H分别为AD、BD、BC、AC的中点,顺次连结点E、F、G、H,所得四边形是一个怎样的四边形?请说明理由;若四边形EFGH是一个菱形,则四边形ABCD应满足什么条件?