Question

【题目】如图，直线l分别交x轴、y轴于点A、B，交曲线y= （x>0）于点C，若AB：AC=1:3，且S△AOB= ，则k的值为（ ）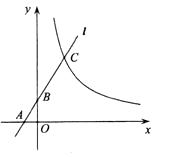

A.
B.2
C.
D.

Answer 1

【答案】A
【解析】解：过C作CD⊥y轴于点D，连接OC，如图，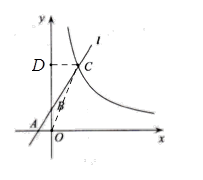

∵∠AOB=∠CDB=90°，∠ABO=∠CBD，
∴△AOB~△CDB，
∴ ，则 ，
∵S△AOB= ，∴S△CDB= ，
由OB：BD=1:2，可得S△OBC= S△CDB= ，
则k=2（S△OBC+ S△CDB）= .
故选A.
【考点精析】认真审题，首先需要了解反比例函数的性质(性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大)．