题目内容
【题目】已知抛物线![]() .
.
(1)当顶点坐标为![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(2)当![]() 时,
时,![]() ,
,![]() 是抛物线图象上的两点,且
是抛物线图象上的两点,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若抛物线上的点![]() ,满足
,满足![]() 时,
时,![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() ;(3)
;(3) ![]() 或
或![]()
【解析】分析:(1)利用抛物线的顶点坐标公式即可得出结论;
(2)先确定出抛物线对称轴x=﹣1,进而得出点Q的坐标,即可得出结论;
(3)分三种情况利用抛物线的增减性建立方程组即可得出结论.
详解:(1)由已知得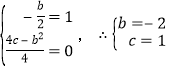 ,
,
∴抛物线的解析式为 y=x2﹣2x+1;
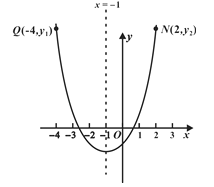
(2)当b=2时,y=x2+2x+c, ∴对称轴直线x=﹣1.
由图取抛物线上点Q,使Q与N关于对称轴x=﹣1对称,由N(2,y2)得Q(﹣4,y2).
又∵M(m,y1)在抛物线图象上的点,且y1>y2,由函数增减性得:m<﹣4或m>2;
(3)分三种情况:
①当﹣![]() <﹣1,即b>2时,函数值y随x的增大而增大,依题意有:
<﹣1,即b>2时,函数值y随x的增大而增大,依题意有:![]()
②当﹣1≤﹣![]() ≤1,即﹣2≤b≤2时,x=﹣
≤1,即﹣2≤b≤2时,x=﹣![]() 时,函数值y取最小值,分两种情况讨论:
时,函数值y取最小值,分两种情况讨论:
(ⅰ)若0≤﹣![]() ≤1,即﹣2≤b≤0时,依题意有:
≤1,即﹣2≤b≤0时,依题意有:
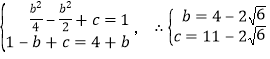 或
或![]() (舍去)
(舍去)
(ⅱ)若﹣1≤﹣![]() ≤0,即0≤b≤2时,依题意有
≤0,即0≤b≤2时,依题意有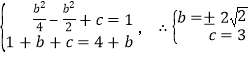 (舍去)
(舍去)
③当﹣![]() >1,即b<﹣
>1,即b<﹣![]() (舍去)
(舍去)
综上所述:![]() 或
或![]() .
.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】某电器超市销售每台进价为120元、170元的A,B两种型号的电风扇,如表所示是近2周的销售情况:(进价、售价均保持不变,利润=销售收入一进货成本)
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 6 | 5 | 2200元 |
第二周 | 4 | 10 | 3200元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市再采购这两种型号的电风扇共130台,并且全部销售完,该超市能否实现这两批的总利润为8010元的目标?若能,请给出相应的采购方案;若不能,请说明理由.