题目内容
 如图,点E在正方形ABCD的边BC的延长线上,如果BE=BD,AB=1,那么∠E=
如图,点E在正方形ABCD的边BC的延长线上,如果BE=BD,AB=1,那么∠E=67.5°
67.5°
;CE=| 2 |
| 2 |
分析:由正方形的性质可知∠DBC=45°,再由等腰三角形的性质求∠E;由勾股定理求BD,由等腰三角形的性质得BE=BD,根据CE=BE-BC求解.
解答:解:∵四边形ABCD为正方形,
∴∠DBC=45°,
又∵BE=BD,
∴∠E=
(180°-∠DBC)=67.5°,
由勾股定理,得BD=
=
,
∴CE=BE-BC=BD-BC=
-1.
故答案为:67.5°,
-1.
∴∠DBC=45°,
又∵BE=BD,
∴∠E=
| 1 |
| 2 |
由勾股定理,得BD=
| BC2+CD2 |
| 2 |
∴CE=BE-BC=BD-BC=
| 2 |
故答案为:67.5°,
| 2 |
点评:本题考查了正方形的性质,等腰三角形的性质,三角形内角和定理及勾股定理的运用.关键是熟练掌握特殊三角形、四边形的性质.

练习册系列答案
相关题目
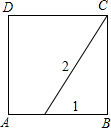 如图,点E在正方形ABCD的边AB上,若EB的长为1,EC的长为2,那么正方形ABCD的面积是( )
如图,点E在正方形ABCD的边AB上,若EB的长为1,EC的长为2,那么正方形ABCD的面积是( )A、
| ||
B、
| ||
| C、3 | ||
| D、5 |
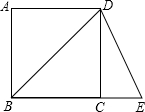 如图,点E在正方形ABCD的边BC的延长线上,如果BE=BD,那么∠E=
如图,点E在正方形ABCD的边BC的延长线上,如果BE=BD,那么∠E=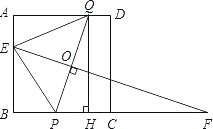 如图,点E在正方形ABCD的边AB上,AE=1,BE=2.点F在边BC的延长线上,且CF=BC;P是边BC上的动点(与点B不重合),PQ⊥EF,垂足为O,并交边AD于点Q;QH⊥BC,垂足为H.
如图,点E在正方形ABCD的边AB上,AE=1,BE=2.点F在边BC的延长线上,且CF=BC;P是边BC上的动点(与点B不重合),PQ⊥EF,垂足为O,并交边AD于点Q;QH⊥BC,垂足为H. (2013•资阳)如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
(2013•资阳)如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )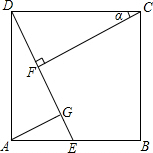 (2013•曲靖)如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.
(2013•曲靖)如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.