题目内容
10.平面直角坐标系中,A(8,0),△AOP为等腰三角形且面积为16,满足条件的第二象限内的点P坐标(-4$\sqrt{3}$,4).分析 使△AOP为等腰三角形,只需分两种情况考虑:OA当底边或OA当腰.当OA是底边时,有2个点;当OA是腰时,有8个点,即可得出答案.
解答 解:∵A(8,0),
∴OA=8,
设△AOP的边OA上的高是h,
则$\frac{1}{2}$×8×h=16,
解得:h=4,
在x轴的两侧作直线a和直线b都和x轴平行,且到x轴的距离都等于4,如图: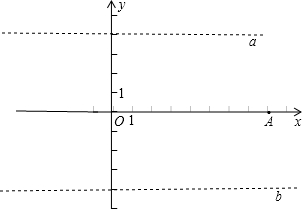
①以A为圆心,以8为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,
②以O为圆心,以8为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,
③作AO的垂直平分线分别交直线a、b于一点,即共2个点符合,
4+4+1+1=10.
满足条件的第二象限内的点P坐标为(-4$\sqrt{3}$,4)
故答案为:(-4$\sqrt{3}$,4)
点评 此题主要考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.

练习册系列答案
相关题目
5.下列四组等式变形中,正确的是( )
| A. | 由$\frac{x}{6}$=2,得x=$\frac{1}{3}$ | B. | 由5x=7.得x=$\frac{5}{7}$ | ||
| C. | 由5x+7=0,得5x=-7 | D. | 由2x-3=0,得2x-3+3=0 |
15.点P(-3,2)关于原点对称的点Q的坐标为( )
| A. | (3,2) | B. | (-3,-2) | C. | (3.-2) | D. | (-3,-2) |
2.如果单项式8x4y|b|与-9xay3是同类项,那么a+b的值为( )
| A. | 7 | B. | 1 | C. | 7和1 | D. | -7 |
19. 如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠COB、∠B 的度数是( )°.
如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠COB、∠B 的度数是( )°.
 如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠COB、∠B 的度数是( )°.
如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠COB、∠B 的度数是( )°.| A. | 10°和40° | B. | 10°和50° | C. | 40°和50° | D. | 10°和60° |
 如图,A、B、C、D在同一条直线上,AB=6,AD=$\frac{1}{3}$AB,CD=1,则BC=3.
如图,A、B、C、D在同一条直线上,AB=6,AD=$\frac{1}{3}$AB,CD=1,则BC=3.