题目内容
如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC :∠BOC = 2:1,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)将图1中的三角板绕点O按顺时针方向旋转至图2的位置,使得OM落在射线OA上,此时ON旋转的角度为 °;
(2)继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置,使得OM在∠BOC的内部,则∠BON-∠COM = °;
(3)在上述直角三角板从图1旋转到图3的位置的过程中,若三角板绕点O按每秒钟15°的速度旋转,当OM恰为∠BOC的平分线时,此时,三角板绕点O的运动时间为 秒,简要说明理由.




解:(1)90;
(2)30; (3)16秒.
理由:如图.
∵ 点O为直线AB上一点,∠AOC :∠BOC = 2:1,
∴ ∠AOC=120°,∠BOC=60°.
∵ OM恰为∠BOC的平分线,
∴ ∠COM’=30°.
∴ ∠AOM +∠AOC+∠COM’=240°.
∵ 三角板绕点O按每秒钟15°的速度旋转,
∴ 三角板绕点O的运动时间为 =16(秒).
=16(秒).


练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
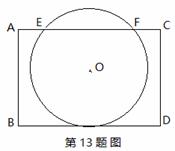
 B.
B. C.2 D.﹣2
C.2 D.﹣2 ),解答下列问题:
),解答下列问题: y的代数式表示地面的总面积(结果要化简);
y的代数式表示地面的总面积(结果要化简); ,且地面总面积是卫生间面积的15倍,铺1
,且地面总面积是卫生间面积的15倍,铺1
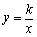 (k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )
(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( ) )
)