题目内容
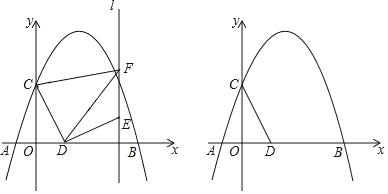
【题目】如图,抛物线y=﹣![]() +bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
+bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
(1)求抛物线解析式;
(2)若线段DE是CD绕点D顺时针旋转90°得到,求线段DF的长;
(3)若线段DE是CD绕点D旋转90°得到,且点E恰好在抛物线上,请求出点E的坐标.
【答案】(1) 抛物线解析式为y=﹣![]() ;(2) DF=3
;(2) DF=3![]() ;(3) 点E的坐标为E1(4,1)或E2(﹣
;(3) 点E的坐标为E1(4,1)或E2(﹣![]() ,﹣
,﹣![]() )或E3(
)或E3(![]() ,﹣
,﹣![]() )或E4(
)或E4(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)将点A、C坐标代入抛物线解析式求解可得;
(2)证△COD≌△DHE得DH=OC,由CF⊥FH知四边形OHFC是矩形,据此可得FH=OC=DH=3,利用勾股定理即可得出答案;
(3)设点D的坐标为(t,0),由(1)知△COD≌△DHE得DH=OC、EH=OD,再分CD绕点D顺时针旋转和逆时针旋转两种情况,表示出点E的坐标,代入抛物线求得t的值,从而得出答案.
(1)∵抛物线y=﹣![]() +bx+c交x轴于点A(﹣2,0)、C(0,3),∴
+bx+c交x轴于点A(﹣2,0)、C(0,3),∴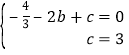 ,解得:
,解得:![]() ,∴抛物线解析式为y=﹣
,∴抛物线解析式为y=﹣![]() +
+![]() x+3;
x+3;
(2)如图1.
∵∠CDE=90°,∠COD=∠DHE=90°,∴∠OCD+∠ODC=∠HDE+∠ODC,∴∠OCD=∠HDE.
又∵DC=DE,∴△COD≌△DHE,∴DH=OC.
又∵CF⊥FH,∴四边形OHFC是矩形,∴FH=OC=DH=3,∴DF=3![]() ;
;
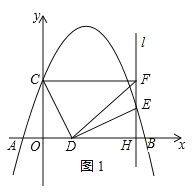
(3)如图2,设点D的坐标为(t,0).
∵点E恰好在抛物线上,且EH=OD,∠DHE=90°,∴由(2)知,△COD≌△DHE,∴DH=OC,EH=OD,分两种情况讨论:
①当CD绕点D顺时针旋转时,点E的坐标为(t+3,t),代入抛物线y=﹣![]() +
+![]() x+3,得:﹣
x+3,得:﹣![]() (t+3)2+
(t+3)2+![]() (t+3)+3=t,解得:t=1或t=﹣
(t+3)+3=t,解得:t=1或t=﹣![]() ,所以点E的坐标E1(4,1)或E2(﹣
,所以点E的坐标E1(4,1)或E2(﹣![]() ,﹣
,﹣![]() );
);
②当CD绕点D逆时针旋转时,点E的坐标为(t﹣3,﹣t),代入抛物线y=﹣![]() +
+![]() x+3得:﹣
x+3得:﹣![]() (t﹣3)2+
(t﹣3)2+![]() (t﹣3)+3=﹣t,解得:t=
(t﹣3)+3=﹣t,解得:t=![]() 或t=
或t=![]() .故点E的坐标E3(
.故点E的坐标E3(![]() ,﹣
,﹣![]() )或E4(
)或E4(![]() ,﹣
,﹣![]() );
);
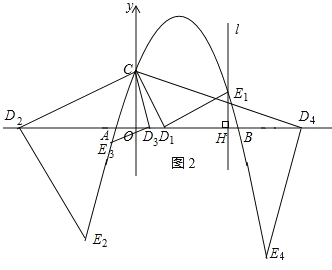
综上所述:点E的坐标为E1(4,1)或E2(﹣![]() ,﹣
,﹣![]() )或E3(
)或E3(![]() ,﹣
,﹣![]() )或E4(
)或E4(![]() ,﹣
,﹣![]() ).
).

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案