题目内容
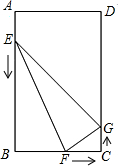 (2011•聊城)如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动.点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2)
(2011•聊城)如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动.点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2)(1)当t=1秒时,S的值是多少?
(2)写出S和t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点E、B、F为顶点的三角形与以点F、C、G为顶点的三角形相似?请说明理由.
分析:(1)当t=1时,根据点E、G的速度均为2cm/s,点F的速度为4cm/s,可求出S和t的关系.
(2)根据点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S,求出S和t的关系式.
(3)两边对应成比例夹角相等的三角形是相似三角形可求出解.
(2)根据点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S,求出S和t的关系式.
(3)两边对应成比例夹角相等的三角形是相似三角形可求出解.
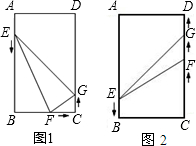
解答:解:(1)如图1,当t=1秒时,AE=2,EB=10,BF=4,FC=4,CG=2----------(1分)
由S=S梯形GCBE-S△EBF-S△FCG----------(2分)
=
×(EB+CG)•BC-
EB•BF-
FC•CG
=
×(10+2)×8-
×10×4-
×4×2
=24(cm2)----------(3分)
(2)①如图1,当0≤t≤2时,点E、F、G分别在边AB、BC、CD上移动,
此时AE=2t,EB=12-2t,BF=4t,FC=8-4t,CG=2t
S=S梯形GCBE-S△EBF-S△FCG
=
×(EB+CG)•BC-
EB•BF-
FC•CG
=
×8×(12-2t+2t)-
×4t(12-2t)-
×2t(8-4t)
=8t2-32t+48.----------(4分)
②如图2,当点F追上点G时,4t=2t+8,解得t=4----------(5分)
当2<t<4时,点E在边AB上移动,点F、G都在边CD上移动,此时CF=4t-8,CG=2t
FG=CG-CF=2t-(4t-8)=8-2t
S=
FG•BC=
(8-2t)•8=-8t+32.
即S=-8t+32----------(6分)
(3)如图1,当点F在矩形的边BC上的边移动时,0≤t≤2
在△EBF和△FCG中,∠B=∠C=90°
1若
=
,即
=
,
解得t=
.
又t=
满足0≤t≤2,所以当t=
时,△EBF∽△FCG----------(7分)
2若
=
即
=
,解得t=
.
又t=
满足0≤t≤2,所以当t=
时,△EBF∽△GCF----------(8分)
综上所述,当t=
或t=
时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似.

由S=S梯形GCBE-S△EBF-S△FCG----------(2分)
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=24(cm2)----------(3分)
(2)①如图1,当0≤t≤2时,点E、F、G分别在边AB、BC、CD上移动,
此时AE=2t,EB=12-2t,BF=4t,FC=8-4t,CG=2t
S=S梯形GCBE-S△EBF-S△FCG
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=8t2-32t+48.----------(4分)
②如图2,当点F追上点G时,4t=2t+8,解得t=4----------(5分)
当2<t<4时,点E在边AB上移动,点F、G都在边CD上移动,此时CF=4t-8,CG=2t
FG=CG-CF=2t-(4t-8)=8-2t
S=
| 1 |
| 2 |
| 1 |
| 2 |
即S=-8t+32----------(6分)
(3)如图1,当点F在矩形的边BC上的边移动时,0≤t≤2
在△EBF和△FCG中,∠B=∠C=90°
1若
| EB |
| FC |
| BF |
| CG |
| 12-2t |
| 8-4t |
| 4t |
| 2t |
解得t=
| 2 |
| 3 |
又t=
| 2 |
| 3 |
| 2 |
| 3 |
2若
| EB |
| GC |
| BF |
| CF |
| 12-2t |
| 2t |
| 4t |
| 8-4t |
| 3 |
| 2 |
又t=
| 3 |
| 2 |
| 3 |
| 2 |
综上所述,当t=
| 2 |
| 3 |
| 3 |
| 2 |
点评:本题考查了相似三角形的判定定理,一次函数的应用和三角形的面积以及矩形的性质等知识点.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
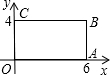 (2011•聊城)如图,矩形OABC的顶点O是坐标原点,边OA在x轴上,边OC在y轴上.若矩形OA1B1C1与矩形OABC关于点O位似,且矩形OA1B1C1的面积等于矩形OABC面积的
(2011•聊城)如图,矩形OABC的顶点O是坐标原点,边OA在x轴上,边OC在y轴上.若矩形OA1B1C1与矩形OABC关于点O位似,且矩形OA1B1C1的面积等于矩形OABC面积的 (2011•聊城)如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为( )
(2011•聊城)如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为( )
 轴于点C.
轴于点C. (2011•聊城)如图,在平行四边形ABCD中,AC、BD相交于点O,点E是AB的中点.若OE=3cm,则AD的长是
(2011•聊城)如图,在平行四边形ABCD中,AC、BD相交于点O,点E是AB的中点.若OE=3cm,则AD的长是