题目内容
 如图,已知正方形纸片ABCD的边长为8,O是正方形的中心,⊙O的半径为2.沿EF折叠纸片,使点A落在⊙O上的A1处,且EA1所在直线与⊙O只有一个公共点A1,延长FA1交CD边于点G,则A1G的长是
如图,已知正方形纸片ABCD的边长为8,O是正方形的中心,⊙O的半径为2.沿EF折叠纸片,使点A落在⊙O上的A1处,且EA1所在直线与⊙O只有一个公共点A1,延长FA1交CD边于点G,则A1G的长是
- A.

- B.6
- C.

- D.

A
分析:根据翻折变换得到EA1是⊙0的切线,然后利用切线的性质,有FG⊥EA1,因为点O是正方形的中心,所以AF=CG,再过点G作AB的垂线交AB于H,在△FGH中用勾股定理计算求出线段AF的长,然后得到A1G的长.
解答: 解:如图:过点G作GH⊥AB于点H,
解:如图:过点G作GH⊥AB于点H,
∵∠A=90°,∴∠EA1F=90°,
∵EA1所在的直线与⊙0只有一个公共点,
∴EA1是⊙0的切线,
∵点O是正方形ABCD的中心,
∴AF=CG
设AF=a,则FA1=a,CG=a,
在直角△FGH中,
FH=8-2a,HG=8,FG=4+2a,
∴(4+2a)2=(8-2a)2+82,
解得:a=
∴A1G=4+a= .
.
故选A.
点评:本题考查的是切线的性质,利用翻折原理得到直线EA1是圆的切线,然后利用切线的性质和正方形的性质,通过作辅助线得到直角三角形,在直角三角形中利用勾股定理求出线段的长.
分析:根据翻折变换得到EA1是⊙0的切线,然后利用切线的性质,有FG⊥EA1,因为点O是正方形的中心,所以AF=CG,再过点G作AB的垂线交AB于H,在△FGH中用勾股定理计算求出线段AF的长,然后得到A1G的长.
解答:
 解:如图:过点G作GH⊥AB于点H,
解:如图:过点G作GH⊥AB于点H,∵∠A=90°,∴∠EA1F=90°,
∵EA1所在的直线与⊙0只有一个公共点,
∴EA1是⊙0的切线,
∵点O是正方形ABCD的中心,
∴AF=CG
设AF=a,则FA1=a,CG=a,
在直角△FGH中,
FH=8-2a,HG=8,FG=4+2a,
∴(4+2a)2=(8-2a)2+82,
解得:a=

∴A1G=4+a=
 .
.故选A.
点评:本题考查的是切线的性质,利用翻折原理得到直线EA1是圆的切线,然后利用切线的性质和正方形的性质,通过作辅助线得到直角三角形,在直角三角形中利用勾股定理求出线段的长.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
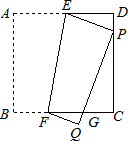 与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.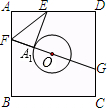 如图,已知正方形纸片ABCD的边长为8,O是正方形的中心,⊙O的半径为2.沿EF折叠纸片,使点A落在⊙O上的A1处,且EA1所在直线与⊙O只有一个公共点A1,延长FA1交CD边于点G,则A1G的长是( )
如图,已知正方形纸片ABCD的边长为8,O是正方形的中心,⊙O的半径为2.沿EF折叠纸片,使点A落在⊙O上的A1处,且EA1所在直线与⊙O只有一个公共点A1,延长FA1交CD边于点G,则A1G的长是( )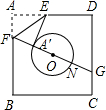 如图,已知正方形纸片ABCD的边长为8,⊙0的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙0相切于点A′(△EFA′与⊙0除切点外无重叠部分),延长FA′交CD边于点G,则A′G的长是
如图,已知正方形纸片ABCD的边长为8,⊙0的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙0相切于点A′(△EFA′与⊙0除切点外无重叠部分),延长FA′交CD边于点G,则A′G的长是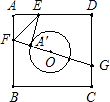 如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A′(△EFA′与⊙O除切点外无重叠部分),延长FA′交CD边于点G,求A′G的长.
如图,已知正方形纸片ABCD的边长为8,⊙O的半径为2,圆心在正方形的中心上,将纸片按图示方式折叠,使EA恰好与⊙O相切于点A′(△EFA′与⊙O除切点外无重叠部分),延长FA′交CD边于点G,求A′G的长.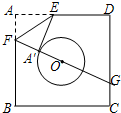 如图,已知正方形纸片ABCD的边长为4,⊙O的半径为1,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙O相切于点A′,延长F A′交CD边于点G,则A′G的长是
如图,已知正方形纸片ABCD的边长为4,⊙O的半径为1,圆心在正方形的中心上,将纸片按图示方式折叠,使E A′恰好与⊙O相切于点A′,延长F A′交CD边于点G,则A′G的长是