题目内容
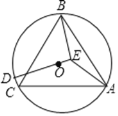
【题目】如图，△ABC为⊙O的内接等边三角形，BC=12，点D为
上一动点，BE⊥OD于E，当点D由点B沿运动到点C时，线段AE的最大值是（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
连接BO，取BO中点M，连接ME，点E在以M为圆心，BM为半径的圆上，由△ABC是等边三角形可得AH=BH=6，BH=6
，BO=MH=4，BM=2，根据勾股定理可得AM的长即
可求AE的最大值．
解：如图
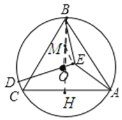
连接BO，取BO中点M，连接ME
∵DE⊥BE，M是BO中点
∴ME=
BO
∴E在以M为圆心，BM为半径的圆上
∴当A，M，E共线且E在AM的延长线上时，AE的值最大
延长BO交AC于H
∵△ABC为⊙O的内接等边三角形
∴HB⊥AC，且△ABC是等边三角形，BC=12
∴CH=AH=6
∴AH=6 ，AO=4，BH=6
则OM=2，MH=4
∴AM=
∴AE的最大值为2
+2
故选：A．
练习册系列答案
相关题目
