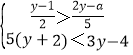题目内容
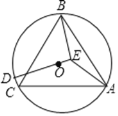
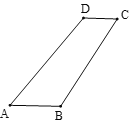
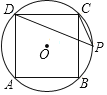
【题目】如图,正方形ABCD内接于⊙O,P为![]() 上一点,连接PD、PC.
上一点,连接PD、PC.
(1)∠CPD=______°.
(2)若DC=4,CP=2![]() ,求DP的长.
,求DP的长.
【答案】(1)45;(2)DP= 2+![]() .
.
【解析】
(1)连接BD,根据正方形ABCD内接于⊙O,可得∠CPD=∠DBC=45°;
(2)作CH⊥DP于H,因为CP=2![]() ,∠CPD=45°,可得CH=PH=2,因为DC=4,所以DH=
,∠CPD=45°,可得CH=PH=2,因为DC=4,所以DH=![]() ,即DP=PH+DH=2+
,即DP=PH+DH=2+![]() .
.
(1)如图,连接BD,

∵正方形ABCD内接于⊙O,P为![]() 上一点,
上一点,
∴∠DBC=45°,
∵∠CPD=∠DBC,
∴∠CPD=45°,
故答案为:45°;
(2)如图,作CH⊥DP于H,
∵CP=2![]() ,∠CPD=45°,
,∠CPD=45°,
∴CH=PH=2,
∵DC=4,
∴DH=![]() ,
,
∴DP=PH+DH=2+2![]() .
.

练习册系列答案
相关题目
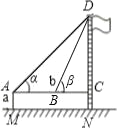
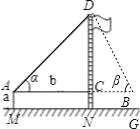
【题目】某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
课题 | 测量校内旗杆高度 | ||
目的 | 运用所学数学知识及数学方法解决实际问题﹣﹣﹣测量旗杆高度 | ||
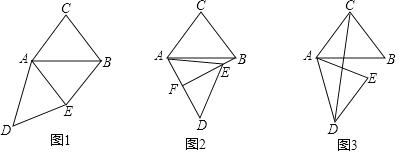
方案 | 方案一 | 方案二 | 方案三 |
示意图 |
|
| |
测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
计算过程(结 果保留根号) | 解: | 解: | |
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)