Question

某公司购进一种化工原料若干千克，价格为每千克30元，物价部门规定其销售单价每千克不高于60元且不低于30元，经市场调查发现，日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时，y=80，当x=50时，y=100．

（1）求y与x的函数解析式；

（2）求该公司销售该原料日获利w（元）与销售单价x（元）之间的函数解析式；

（3）求当销售单价为多少元时，该公司日获利最大？最大利润是多少元？

Answer 1

【考点】二次函数的应用．

【专题】销售问题．

【分析】（1）根据日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时，y=80，当x=50时，y=100，可以求得y与x的函数解析式；

（2）根据公司购进一种化工原料若干千克，价格为每千克30元，物价部门规定其销售单价每千克不高于60元且不低于30元，和第一问中求得的y与x的函数解析式，可以求得该公司销售该原料日获利w（元）与销售单价x（元）之间的函数解析式；

（3）将第（2）问中的函数解析式化为顶点式，然后根据二次项系数和对称轴和x的取值范围可以确定当销售单价为多少元时，该公司日获利最大，最大利润是多少元．

【解答】解；（1）由题意可得，设y与x的函数解析式是：y=kx+b，

∵当x=60时，y=80，当x=50时，y=100，

∴，

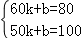解得k=﹣2，b=200．

即y与x的函数解析式是：y=﹣2x+200（30≤x≤60）；

（2）由题意可得，

w=（x﹣30）（﹣2x+200）=﹣2x²+260x﹣6000，

即该公司销售该原料日获利w（元）与销售单价x（元）之间的函数解析式是：w=﹣2x²+260x﹣6000；

（3）∵w=﹣2x²+260x﹣6000

∴w=﹣2（x﹣65）²+2450

∴当x＜65时，y随x的增大而增大，

∵30≤x≤60，

∴当x=60时，w取得最大值，此时w=﹣2（60﹣65）²+2450=2400（元），

即当销售单价为60元时，该公司日获利最大，最大利润是2400元．

【点评】本题考查二次函数的应用，解题的关键是明确题意列出相应的函数解析式，可以将二次函数解析式化为顶点式，根据函数图象的性质解答问题．