题目内容
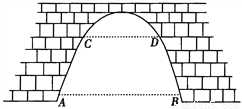
如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
题目内容
如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案