题目内容
7.已知矩形纸片ABCD中,AB=6,BC=$2\sqrt{3}$,将该矩形纸片沿对角线AC剪开,得到两张三角形纸片(如图1),再将这两张三角形纸片摆成如图2的形状,使得点B、C、F、D在同一直线上,且点C与点F重合.此时将△ABC以每秒1个单位长度的速度沿直线BD向左平移,直至点B与点D重合时停止运动.设△ABC运动的时间为t,(1)当t为何值时,点E落在线段AC上?
(2)设在平移的过程中△ABC与△DEF重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出相对应t的取值范围;
(3)当点B与点D重合时如图3,将△ABC绕点B旋转得到△A1BC1,直线EF分别与直线A1B、直线A1C1交于点M、N,是否存在这样的点M、N,使得△A1MN为等腰三角形?若存在,请求出此时线段EM的长度;若不存在,请说明理由.

分析 (1)当点E落在AC上时,解Rt△CDE,由CD=t-6,DE=2$\sqrt{3}$,∠DCE=60°,可得$\sqrt{3}$CD=DE,即$\sqrt{3}$(t-6)=2$\sqrt{3}$,解方程即可;
(2)△ABC沿直线BD向左平移时,因为△ABC与△DEF重叠部分的形状不同,可以分四种情况进行讨论:①当0≤t≤2$\sqrt{3}$时,重叠部分为直角三角形CMF;②当2$\sqrt{3}$<t≤6时,重叠部分为四边形BCNM;③当6<t≤8时,重叠部分为五边形BDPNM;④当8<t≤6+2$\sqrt{3}$时,重叠部分为直角梯形BMED;分别求出面积即可;
(3)当点B与点D重合时,如果△A1MN为等腰三角形,可分三种情况进行讨论:①A1M=A1N;②MA1=MN;③NA1=NM.
解答 解:(1)由题意知,Rt△ABC与Rt△DEF中,∠CAB=∠DFE=30°.
当点E落在AC上时,CD=t-6,DE=2$\sqrt{3}$,∠DCE=60°,
则$\sqrt{3}$CD=DE,即$\sqrt{3}$(t-6)=2$\sqrt{3}$,
解得t=8; (2)分四种情况:
(2)分四种情况:
①当0≤t≤2$\sqrt{3}$时,如图1.
在△CFM中,
∵∠MCF=60°,∠CFM=30°,
∴∠CMF=90°,
∵CF=t,
∴CM=$\frac{1}{2}$t,FM=$\frac{\sqrt{3}}{2}$t,
∴S=$\frac{1}{2}$CM•FM=$\frac{1}{2}$•$\frac{1}{2}$t•$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{8}$t2;
②当2$\sqrt{3}$<t≤6时,如图2.
在Rt△BFM中,
∵∠F=30°,BF=CF-BC=t-2$\sqrt{3}$,
∴BM=$\frac{\sqrt{3}}{3}$BF=$\frac{\sqrt{3}}{3}$t-2,
∴AM=AB-BM=6-$\frac{\sqrt{3}}{3}$t+2=8-$\frac{\sqrt{3}}{3}$t,
∴MN=$\frac{1}{2}$AM=4-$\frac{\sqrt{3}}{6}$t,AN=$\sqrt{3}$MN=4$\sqrt{3}$-$\frac{1}{2}$t,
∴S=S△ABC-S△AMN
=$\frac{1}{2}$×6×2$\sqrt{3}$-$\frac{1}{2}$×(4-$\frac{\sqrt{3}}{6}$t)(4$\sqrt{3}$-$\frac{1}{2}$t)
=-$\frac{\sqrt{3}}{24}$t2+2t-2$\sqrt{3}$;
③当6<t≤8时,如图3.
在Rt△CDP中,
∵∠CPD=30°,CD=t-6, ∴PD=$\sqrt{3}$CD=$\sqrt{3}$(t-6),
∴PD=$\sqrt{3}$CD=$\sqrt{3}$(t-6),
∴S=S△ABC-S△AMN-S△CPD
=-$\frac{\sqrt{3}}{24}$t2+2t-2$\sqrt{3}$-$\frac{1}{2}$×$\sqrt{3}$(t-6)×(t-6)
=-$\frac{13\sqrt{3}}{24}$t2+(6$\sqrt{3}$+2)t-20$\sqrt{3}$;
④当8<t≤6+2$\sqrt{3}$时,如图4.
∵CD=t-6,
∴BD=BC-CD=2$\sqrt{3}$+6-t.
在Rt△BFM中,
∵∠F=30°,BF=CF-BC=t-2$\sqrt{3}$,
∴BM=$\frac{\sqrt{3}}{3}$BF=$\frac{\sqrt{3}}{3}$t-2,
∴S=$\frac{1}{2}$(BM+DE)•BD
=$\frac{1}{2}$($\frac{\sqrt{3}}{3}$t-2+2$\sqrt{3}$)(2$\sqrt{3}$+6-t)
=-$\frac{\sqrt{3}}{6}$t2+2t+4$\sqrt{3}$;
综上所述,S与t之间的函数关系式为: $S=\left\{\begin{array}{l}\frac{{\sqrt{3}}}{8}{t^2}(0≤t≤2\sqrt{3})\\-\frac{{\sqrt{3}}}{24}{t^2}+2t-2\sqrt{3}(2\sqrt{3}<t≤6)\\-\frac{13}{24}\sqrt{3}{t^2}+(6\sqrt{3}+2)t-20\sqrt{3}(6<t≤8)\\-\frac{{\sqrt{3}}}{6}{t^2}+2t+4\sqrt{3}(8<t≤6+2\sqrt{3})\end{array}\right.$;
$S=\left\{\begin{array}{l}\frac{{\sqrt{3}}}{8}{t^2}(0≤t≤2\sqrt{3})\\-\frac{{\sqrt{3}}}{24}{t^2}+2t-2\sqrt{3}(2\sqrt{3}<t≤6)\\-\frac{13}{24}\sqrt{3}{t^2}+(6\sqrt{3}+2)t-20\sqrt{3}(6<t≤8)\\-\frac{{\sqrt{3}}}{6}{t^2}+2t+4\sqrt{3}(8<t≤6+2\sqrt{3})\end{array}\right.$;
(3)存在这样的点M、N,理由如下:
由题意得△A1MN∽△FMB,
即当△A1MN为等腰三角形时,△FMB也为等腰三角形.
①如图5,当A1M=A1N时,即FB=FM=6, 若点M在线段EF上时,EM=EF-FM=4$\sqrt{3}$-6;
若点M在线段EF上时,EM=EF-FM=4$\sqrt{3}$-6;
若点M在线段EF的延长线上时,EM=EF+FM=4$\sqrt{3}$+6;
②如图6,当MA1=MN时,即MB=MF,则点M在线段BF的中垂线上,过M作MT⊥BF于点T,则BT=FT=3,
∴MT=$\sqrt{3}$,MF=$2\sqrt{3}$,
∴EM=EF-MF=4$\sqrt{3}$-$2\sqrt{3}$=$2\sqrt{3}$;
③当NA1=NM时,即BM=BF=6,但是BA1=BF=6,所以A1、M、N三点重合,不合题意;
综上所述,存在这样的点M、N,使得△A1MN为等腰三角形,此时线段EM的长度为4$\sqrt{3}$-6或4$\sqrt{3}$+6或$2\sqrt{3}$.
点评 本题是几何变换综合题,其中涉及到矩形的性质,平移的性质,多边形的面积,解直角三角形,等腰三角形的性质,有一定难度.运用数形结合、分类讨论及方程思想是解题的关键.

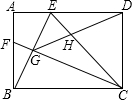 如图,在矩形ABCD中,E是AD边上的一点,CF垂直平分BE于点G,交AB于点F,连接DG、CE交于点H.若DE=2AE,则给出下列结论:①DG=CG;②3AF=2BF;③DG平分∠EGC;④EH=$\frac{{\sqrt{30}}}{10}$HD.其中正确的结论是( )
如图,在矩形ABCD中,E是AD边上的一点,CF垂直平分BE于点G,交AB于点F,连接DG、CE交于点H.若DE=2AE,则给出下列结论:①DG=CG;②3AF=2BF;③DG平分∠EGC;④EH=$\frac{{\sqrt{30}}}{10}$HD.其中正确的结论是( )| A. | 只有①② | B. | 只有①②④ | C. | 只有③④ | D. | ①②③④ |
| A. | ($\frac{5}{2}$,0) | B. | (3,0) | C. | (4,0) | D. | (5,0) |
| A. | 整数 | B. | 分数 | C. | 有理数 | D. | 不是有理数 |
 如图,MN是线段AB的中垂线,MN=6,在MN上取C、D两点,连接AD,AC,BC,S△BMN:S△ADN=2:1,S△ADN:S△BCN=4:3,则CD的长度为$\frac{3}{4}$.
如图,MN是线段AB的中垂线,MN=6,在MN上取C、D两点,连接AD,AC,BC,S△BMN:S△ADN=2:1,S△ADN:S△BCN=4:3,则CD的长度为$\frac{3}{4}$.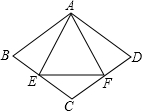 如图,在四边形ABCD中,AB=AD=BC=CD=4,AB∥CD,AD∥BC,∠BAD=120°.△AEF为等边三角形,点E,F分别在BC,CD上滑动,且点E,F不与点B,C,D重合,
如图,在四边形ABCD中,AB=AD=BC=CD=4,AB∥CD,AD∥BC,∠BAD=120°.△AEF为等边三角形,点E,F分别在BC,CD上滑动,且点E,F不与点B,C,D重合,