Question

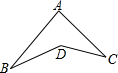
已知如图，在△ABC中，CH是外角∠ACD的角平分线，BH是∠ABC的平分线，∠A=58°，求∠H的度数．

Answer 1

∵∠A=58°，∴∠ABC+∠ACB=180°-∠A=180°-58°=122°…①，
∵BH是∠ABC的平分线，∴∠HBC=

1

2

∠ABC，
∵∠ACD是△ABC的外角，CH是外角∠ACD的角平分线，
∴∠ACH=

1

2

（∠A+∠ABC），
∴∠BCH=∠ACB+∠ACH=∠ACB+

1

2

（∠A+∠ABC），
∵∠H+∠HBC+∠ACB+∠ACH=180°，
∴∠H+

1

2

∠ABC+∠ACB+

1

2

（∠A+∠ABC）=180°，即∠H+（∠ABC+∠ACB）+

1

2

∠A=180°…②，
把①代入②得，∠H+122°+

1

2

×58°=180°，
∴∠H=29°．