题目内容
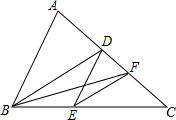
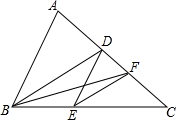如图，BD为△ABC的角平分线，DE∥AB，EF平分∠DEC，下列结论：①∠BDE=∠DBE，②EF∥BD，③CD=CE，④S△BDF=S△BDE．正确的有
- A.①②
- B.①②③
- C.②③④
- D.①②④
D
分析：根据平行线的性质和角平分线的定义对各选项分析判断后利用排除法求解．
解答：∵DE∥AB，
∴∠ABD=∠BDE，∠ABC=∠DEC，
∵BD平分∠ABC，EF平分∠DEC，
∴∠ABD=∠DBE，∠DEF=∠FEC，
∴∠BDE=∠DBE，∠FEC=∠DBC，
∴EF∥BD，
故①②选项正确；
∵AC与BC不一定相等，
∴CD与CE不一定相等，故③选项错误；
∵EF∥BD，
∴△BDF与△BDE是等底等高的三角形，
∴S△BDF=S△BDE，故④选项正确．
所以①②④选项正确．
故选D．
点评：本题主要利用平行线的性质和角平分线的定义求解，熟练掌握性质和概念并灵活运用是解题的关键．
分析：根据平行线的性质和角平分线的定义对各选项分析判断后利用排除法求解．
解答：∵DE∥AB，
∴∠ABD=∠BDE，∠ABC=∠DEC，
∵BD平分∠ABC，EF平分∠DEC，
∴∠ABD=∠DBE，∠DEF=∠FEC，
∴∠BDE=∠DBE，∠FEC=∠DBC，
∴EF∥BD，
故①②选项正确；
∵AC与BC不一定相等，
∴CD与CE不一定相等，故③选项错误；
∵EF∥BD，
∴△BDF与△BDE是等底等高的三角形，
∴S△BDF=S△BDE，故④选项正确．
所以①②④选项正确．
故选D．
点评：本题主要利用平行线的性质和角平分线的定义求解，熟练掌握性质和概念并灵活运用是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
12、如图，BD为△ABC的角平分线，DE∥AB，EF平分∠DEC，下列结论：①∠BDE=∠DBE，②EF∥BD，③CD=CE，④S△BDF=S△BDE．正确的有（ ）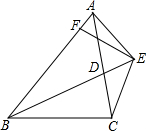
已知：如图，BD为∠ABC的角平分线，且BD=BC，E为BD的延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足，下列结论：①∠ABE=∠ACE；②∠BCE+∠BCD=180°；③AE=EC；④BE+BD=2BF，其中正确的是（ ）
