Question

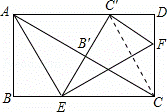
如图，在矩形ABCD中，点E，F分别在BC，CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处．则BC：AB的值为    。

Answer 1

考点：翻折变换（折叠问题）。

解答：解：连接CC′，

∵将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处。

∴EC=EC′，

∴∠EC′C=∠ECC′，

∵∠DC′C=∠ECC′，

∴∠EC′C=∠DC′C，

∴得到CC′是∠EC'D的平分线，

∵∠CB′C′=∠D=90°，

∴CB′=CD，

又∵AB′=AB，

所以B′是对角线AC中点，

即AC=2AB，

所以∠ACB=30°，

∴cot∠ACB=cot30°=，

BC：AB的值为：。

故答案为：。