题目内容
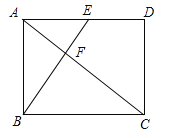
【题目】(2017山东省莱芜市)如图,在矩形ABCD中,BE⊥AC分别交AC、AD于点F、E,若AD=1,AB=CF,则AE=______.
【答案】![]() .
.
【解析】解:∵四边形ABCD是矩形,∴BC=AD=1,∠BAF=∠ABC=90°,∴∠ABE+∠CBF=90°,∵BE⊥AC,∴∠BFC=90°,∴∠BCF+∠CBF=90°,∴∠ABE=∠FCB,在△ABE和△FCB中,∵∠EAB=∠BFC=90°,AB=CF,∠ABE=∠FCB,∴△ABE≌△FCB,∴BF=AE,BE=BC=1,∵BE⊥AC,∴∠BAF+∠ABF=90°,∵∠ABF+∠AEB=90°,∴∠BAF=∠AEB,∵∠BAE=∠AFB,∴△ABE∽△FBA,∴![]() ,∴
,∴![]() ,∴AE=BF=AB2,在Rt△ABE中,BE=1,根据勾股定理得,AB2+AE2=BE2=1,∴AE+AE2=1,∵AE>0,∴AE=
,∴AE=BF=AB2,在Rt△ABE中,BE=1,根据勾股定理得,AB2+AE2=BE2=1,∴AE+AE2=1,∵AE>0,∴AE=![]() .故答案为:
.故答案为:![]() .
.

练习册系列答案
相关题目
【题目】张老师打算在小明和小白两位同学之间选一位同学参加数学竞赛,他收集了小明、小白近期10次数学考试成绩,并绘制了折线统计图(如图所示)
项目 | 众数 | 中位数 | 平均数 | 方差 | 最高分 |
小明 | 85 | 85 | |||
小白 | 70,100 | 85 | 100 |
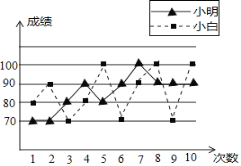
(1)根据折线统计图,张老师绘制了不完整的统计表,请你补充完整统计表;
(2)你认为张老师会选择哪位同学参加比赛?并说明你的理由