题目内容
 如图已知:∠F=∠DAE,∠B=∠D.将AB∥DC的理由补充完整并填写理由.
如图已知:∠F=∠DAE,∠B=∠D.将AB∥DC的理由补充完整并填写理由.
∵∠F=∠DAE(已知),
∴AD∥________,
∴∠D+∠BCE=180°________,
又∵∠B=∠D(已知)
∴∠B+∠BCD=180°________,
∴AB∥DC________.
BF (两直线平行同旁内角互补) (等量代换) (同旁内角互补两直线平行)
分析:由已知的∠F=∠DAE,利用内错角相等两直线平行得到AD与BF平行,再利用两直线平行同旁内角互补得到∠D与∠BCE互补,由∠B=∠D,等量代换得到∠B与∠BCE互补,利用同旁内角互补两直线平行可得出AB与DC平行.
解答:证明:∵∠F=∠DAE(已知),
∴AD∥BF,
∴∠D+∠BCE=180°(两直线平行同旁内角互补),
又∵∠B=∠D(已知),
∴∠B+∠BCD=180° (等量代换),
∴AB∥DC(同旁内角互补两直线平行).
故答案为:BF;(两直线平行同旁内角互补);(等量代换);(同旁内角互补两直线平行)
点评:此题考查了平行线的判定与性质,是一道推理填空题.熟练掌握平行线的判定与性质是解本题的关键.
分析:由已知的∠F=∠DAE,利用内错角相等两直线平行得到AD与BF平行,再利用两直线平行同旁内角互补得到∠D与∠BCE互补,由∠B=∠D,等量代换得到∠B与∠BCE互补,利用同旁内角互补两直线平行可得出AB与DC平行.
解答:证明:∵∠F=∠DAE(已知),
∴AD∥BF,
∴∠D+∠BCE=180°(两直线平行同旁内角互补),
又∵∠B=∠D(已知),
∴∠B+∠BCD=180° (等量代换),
∴AB∥DC(同旁内角互补两直线平行).
故答案为:BF;(两直线平行同旁内角互补);(等量代换);(同旁内角互补两直线平行)
点评:此题考查了平行线的判定与性质,是一道推理填空题.熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 8、如图已知D是△ABC的边BC的中点,过D作两条互相垂直的射线,分别交AB于E,交AC于F,求证:BE+CF>EF.
8、如图已知D是△ABC的边BC的中点,过D作两条互相垂直的射线,分别交AB于E,交AC于F,求证:BE+CF>EF.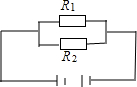 如图已知电阻R1,R2并联在电路中,且R1+R2=10Ω,请用所学过的数学知识讨论一下R1,R2分别为多少时,该电路的总电阻最大,最大电阻是多少?
如图已知电阻R1,R2并联在电路中,且R1+R2=10Ω,请用所学过的数学知识讨论一下R1,R2分别为多少时,该电路的总电阻最大,最大电阻是多少?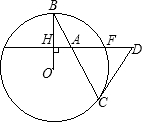 如图已知OB是半径,弦EF垂直OB于H,点A是HF上的一点,BA和⊙O相交于另一点C,过点C的切线和EF的延长线交于点D:
如图已知OB是半径,弦EF垂直OB于H,点A是HF上的一点,BA和⊙O相交于另一点C,过点C的切线和EF的延长线交于点D: 10、如图已知∠ACB=90°,CD⊥AB于D,则图中表示点到直线的距离的线段的条数是( )
10、如图已知∠ACB=90°,CD⊥AB于D,则图中表示点到直线的距离的线段的条数是( ) 如图已知AB∥EF,∠BED=∠B+∠D,求证:AB∥CD
如图已知AB∥EF,∠BED=∠B+∠D,求证:AB∥CD