题目内容
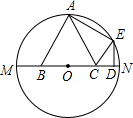 如图,点A、E是⊙O上的点,等边△ABC的边BC与Rt△CDE的边CD都在⊙O的直径MN上,且O为BC的中点,DE⊥CD,CE∥AB,若CD=1,则⊙O的半径为
如图,点A、E是⊙O上的点,等边△ABC的边BC与Rt△CDE的边CD都在⊙O的直径MN上,且O为BC的中点,DE⊥CD,CE∥AB,若CD=1,则⊙O的半径为
- A.

- B.2

- C.2

- D.4
C
分析:延长ED交⊙O于点F,连接OA,OF,由平行线的性质可知∠ECD=60°,故在Rt△ECD中可求出EN的长,再由垂径定理可得出ED=DF,由等边三角形的性质可知AO⊥MN,∠OAC=30°,OA=r,可用r表示出OC的长,在Rt△ODF中,利用勾股定理即可求出r的长.
解答: 解:延长ED交⊙O于点F,连接OA,OF,
解:延长ED交⊙O于点F,连接OA,OF,
∵DE⊥CD,CE∥AB,CD=1,
∴∠ECD=60°,∠CED=30°,
∴CE=2CD=2,
∴ED=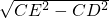 =
= =
= ,
,
∴DF=ED= ,
,
∵△ABC是等边三角形,O为BC的中点,
∴AO⊥MN,
∴∠OAC=30°,
设OA=r,则OC= ,
,
在Rt△ODF中,
OF2=DF2+OD2,即r2=( )2+(
)2+( +1)2,解得r=2
+1)2,解得r=2 .
.
故选C.
点评:本题考查的是垂径定理、勾股定理及等边三角形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
分析:延长ED交⊙O于点F,连接OA,OF,由平行线的性质可知∠ECD=60°,故在Rt△ECD中可求出EN的长,再由垂径定理可得出ED=DF,由等边三角形的性质可知AO⊥MN,∠OAC=30°,OA=r,可用r表示出OC的长,在Rt△ODF中,利用勾股定理即可求出r的长.
解答:
 解:延长ED交⊙O于点F,连接OA,OF,
解:延长ED交⊙O于点F,连接OA,OF,∵DE⊥CD,CE∥AB,CD=1,
∴∠ECD=60°,∠CED=30°,
∴CE=2CD=2,
∴ED=
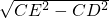 =
= =
= ,
,∴DF=ED=
 ,
,∵△ABC是等边三角形,O为BC的中点,
∴AO⊥MN,
∴∠OAC=30°,
设OA=r,则OC=
 ,
,在Rt△ODF中,
OF2=DF2+OD2,即r2=(
 )2+(
)2+( +1)2,解得r=2
+1)2,解得r=2 .
.故选C.
点评:本题考查的是垂径定理、勾股定理及等边三角形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 6、如图,点A表示的数是2,那么数轴上在A点左侧并且到A点距离为3的点所表示的数是
6、如图,点A表示的数是2,那么数轴上在A点左侧并且到A点距离为3的点所表示的数是 已知:如图,点D、F是△ABC的AB边上的两点,满足AD2=AF•AB,连接CD,过点F作FE∥DC,交边AC于E,连接DE.
已知:如图,点D、F是△ABC的AB边上的两点,满足AD2=AF•AB,连接CD,过点F作FE∥DC,交边AC于E,连接DE.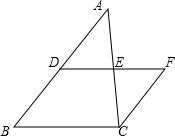 DE=2,EF=y.
DE=2,EF=y. 如图,点D,C是半圆周上的三等分点,直径AB=4,过P作PC∥BD交AB的延长线于点P.
如图,点D,C是半圆周上的三等分点,直径AB=4,过P作PC∥BD交AB的延长线于点P. 如图,点P、Q是直线
如图,点P、Q是直线