题目内容

已知在⊙O中，点A、B、C分别是圆上的三点，且∠AOB=72°，则∠ACB的度数为
36°或144°
36°或144°
度．
分析：首先根据题意画出图形，分别从当点C在优弧上与当点C在劣弧上去分析求解即可求得答案．
解答：解：如图，
当点C在优弧上时，∠ACB=
1
2
∠AOB=
1
2
×72°=36°；
当点C在劣弧上时，∠AC′B=180W°-∠ACB=144°．
则∠ACB的度数为：36°或144°．
故答案为：36°或144°．
点评：此题考查了圆周角定理与圆的内接四边形的性质．此题难度不大，注意掌握数形结合思想与分类讨论思想的应用．
练习册系列答案
相关题目
已知在△ABC中，点D、E分别在边AB和AC上，且DE∥BC，AD：AB=2：3，
AB
=
a
，
AC
=
b
，那么
DE
=
 
（用
a
、
b
表示）．
如图1，已知在⊙O中，点C为劣弧AB上的中点，连接AC并延长至D，使CD=CA，连接DB并延长DB交⊙O于点E，连接AE．
（1）求证：AE是⊙O的直径；
（2）如图2，连接EC，⊙O半径为5，AC的长为4，求阴影部分的面积之和．（结果保留π与根号）
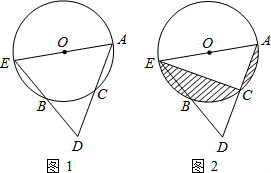
精英家教网
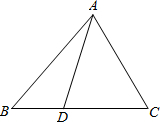（2012•上海模拟）如图，已知在△ABC中，点D在边BC上，且BD：DC=1：2．如果
.
AB
=
.
a
，
.
AC
=
.
b
，那么
.
AD
=
2
3
.
a
+
1
3
.
b
2
3
.
a
+
1
3
.
b
（结果用含
.
a
、
.
b
的式子表示）．
（2014•金山区一模）已知在△ABC中，点D、E分别在边AB、AC上，DE∥BC，
AD
AB
=
3
5
，那么
AE
CE
的值等于
3
2
3
2
．
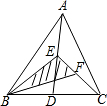已知在△ABC中，点D、E、F分别为BC、AD、CE的中点，且S△ABC=6cm2，则S△BEF的值为
1.5
1.5
cm2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网