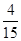题目内容
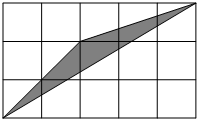
 如果菲菲将镖随意投中如图所示的长方形木板(由15个小正方形组成,假设投中每个小正方形是等可能的),那么镖落在阴影部分的概率为
如果菲菲将镖随意投中如图所示的长方形木板(由15个小正方形组成,假设投中每个小正方形是等可能的),那么镖落在阴影部分的概率为
- A.

- B.

- C.

- D.

A
分析:根据几何概率的求法:镖落在阴影部分的概率就是阴影区域的面积与总面积的比值.
解答:设小正方形面积为1,观察图形可得,图形中共15个小正方形,则总面积为15,
其中阴影部分面积为:2×2÷2+(2+3)×3÷2-3×5÷2=2,
则投中阴影部分的概率为: .
.
故选A.
点评:本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.
分析:根据几何概率的求法:镖落在阴影部分的概率就是阴影区域的面积与总面积的比值.
解答:设小正方形面积为1,观察图形可得,图形中共15个小正方形,则总面积为15,
其中阴影部分面积为:2×2÷2+(2+3)×3÷2-3×5÷2=2,
则投中阴影部分的概率为:
 .
.故选A.
点评:本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如果菲菲将镖随意投中如图所示的长方形木板(由15个小正方形组成,假设投中每个小正方形是等可能的),那么镖落在阴影部分的概率为( )
如果菲菲将镖随意投中如图所示的长方形木板(由15个小正方形组成,假设投中每个小正方形是等可能的),那么镖落在阴影部分的概率为( )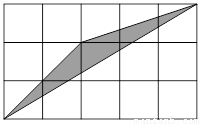
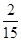 B.
B. 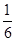 C.
C.
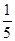 D.
D.