题目内容
12．
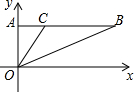如图，在平面直角坐标系中，△OAB的顶点A、B的坐标分别为（0，1）、（2，1），点C在边AB上（不与点B重合），设点C的横坐标为m，△BOC的面积为S，则下面能够反映S与m之间的函数关系的图象是（ ）| A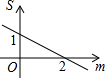． |  | B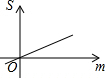． |  | C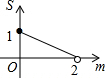． |  | D． |  |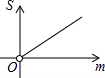
分析 根据函数图象可知OA=2，BC=2-m，从而可以表示出三角形BOC的面积，从而可以得到S与m之间的函数图象，且0≤m＜2．
解答 解：由题意可得，${S}_{△BOC}=\frac{BC×OA}{2}=\frac{（2-m）×2}{2}$=2-m，
所以，S随着m的增大而减小，当m=0时，取得最大值2，m的取值范围是0≤m＜2，
故选C．
点评 本题考查动点问题的函数图象，解题的关键是明确题意，可以表示出三角形的面积关系式，利用数形结合的思想解答问题．
练习册系列答案
相关题目
3．计算（-2a）2的结果是（ ）
| A． | -4a2 | B． | 2a2 | C． | -2a2 | D． | 4a2 |
20．长春市轻轨3号线开通以来，极大缓解了城市的交通压力，据统计，每天轻轨的运载人数为16600人次，16600这个数用科学记数法表示为（ ）
| A． | 16.6×103 | B． | 1.66×104 | C． | 166×102 | D． | 1.66×105 |
甲、乙两车从A地驶向B地，甲车比乙车早行驶2h，并且在途中休息了0.5h，休息前后速度相同，如图是甲、乙两车行驶的距离y（km）与时间x（h）的函数图象．
4．
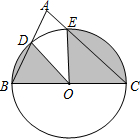如图，以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E．若∠A=80°，BC=4，则图中阴影部分图形的面积和为（ ）
如图，以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E．若∠A=80°，BC=4，则图中阴影部分图形的面积和为（ ）| A． | $\frac{64}{9}π$ | B． | $\frac{32}{9}π$ | C． | $\frac{16}{9}π$ | D． | $\frac{8}{9}π$ |
