题目内容
用长为10米的绳子在一块平地上按下列要求围成一个封闭图形,试求每种情况下所得图形的面积,并指出面积最大的图形的名称.
(1)长比宽多的1米的长方形;
(2)正方形;
(3)圆.
解:(1)设宽为x米,则长为(x+1)米,由题意,得
2×[x+(x+1)]=10,
解得:x=2,
∴长方形的长为:2+1=3,
∴长方形的周长为:2×3=6米2;
(2)由题意,得
正方形的边长为:10÷4=2.5,
正方形的面积为:2.52=6.25米2;
(3)设圆的半径为r米,由题意,得
2πr=10,
r=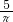 ,
,
∴元的面积为:π• =
= 米2.
米2.
∵6<6.25< ,
,
∴圆的面积最大.
分析:(1)设宽为x米,则长为(x+1)米,由长方形的周长为10建立方程求出其解就可以得出长方形的面积;
(2)先由周长等于10,求出正方形的边长就可以求出正方形的面积;
(3)设圆的半径为r,由圆的周长公式求出半径就可以求出面积,再比较三种图形的面积的大小就可以得出结论.
点评:本题考查了长方形、正方形和圆的周长公式的运用,面积公式的运用,解答时灵活运用基本平面图形的面积计算公式是关键.
2×[x+(x+1)]=10,
解得:x=2,
∴长方形的长为:2+1=3,
∴长方形的周长为:2×3=6米2;
(2)由题意,得
正方形的边长为:10÷4=2.5,
正方形的面积为:2.52=6.25米2;
(3)设圆的半径为r米,由题意,得
2πr=10,
r=
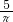 ,
,∴元的面积为:π•
 =
= 米2.
米2.∵6<6.25<
 ,
,∴圆的面积最大.
分析:(1)设宽为x米,则长为(x+1)米,由长方形的周长为10建立方程求出其解就可以得出长方形的面积;
(2)先由周长等于10,求出正方形的边长就可以求出正方形的面积;
(3)设圆的半径为r,由圆的周长公式求出半径就可以求出面积,再比较三种图形的面积的大小就可以得出结论.
点评:本题考查了长方形、正方形和圆的周长公式的运用,面积公式的运用,解答时灵活运用基本平面图形的面积计算公式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 使CE=
使CE= CA,在BC的延长线上取一点E,使CE=
CA,在BC的延长线上取一点E,使CE= CB,测得DE的长为5米,则AB两点间的距离为( )
CB,测得DE的长为5米,则AB两点间的距离为( )
 CA,在BC的延长线上取一点E,使CE=
CA,在BC的延长线上取一点E,使CE= CB,测得DE的长为5米,则AB两点间的距离为( )
CB,测得DE的长为5米,则AB两点间的距离为( )