题目内容
抛物线y=x2+kx+k+3，根据下面的条件，求k的值．
（1）抛物线的顶点在y轴上；
（2）抛物线的顶点在x轴上；
（3）抛物线经过原点；
（4）抛物线的对称轴x=-3．
解：（1）抛物线的顶点在y轴上，即x=-
=0，解得：k=0；
（2）抛物线的顶点在x轴上，即
=0，解得：k=-2或6；
（3）抛物线经过原点，即k+3=0，解得k=-3；
（4）抛物线的对称轴x=-3即：x=-=-3，解得：k=6．
分析：根据二次函数的顶点坐标公式解答即可．
（1）抛物线的顶点在y轴上，即x=-=0，解之即可；
（2）抛物线的顶点在x轴上，即=0，解之即可得出答案；
（3）抛物线经过原点，即k+3=0，解之即可；
（4）抛物线的对称轴x=-3即：x=-=-3．
点评：本题考查了二次函数的最值及图象上点的坐标特征，属于基础题，关键是掌握二次函数上点的坐标特征及二次函数的性质．
=0，解得：k=0；（2）抛物线的顶点在x轴上，即
=0，解得：k=-2或6；（3）抛物线经过原点，即k+3=0，解得k=-3；
（4）抛物线的对称轴x=-3即：x=-
=-3，解得：k=6．分析：根据二次函数的顶点坐标公式解答即可．
（1）抛物线的顶点在y轴上，即x=-
=0，解之即可；（2）抛物线的顶点在x轴上，即
=0，解之即可得出答案；（3）抛物线经过原点，即k+3=0，解之即可；
（4）抛物线的对称轴x=-3即：x=-
=-3．点评：本题考查了二次函数的最值及图象上点的坐标特征，属于基础题，关键是掌握二次函数上点的坐标特征及二次函数的性质．
练习册系列答案
相关题目
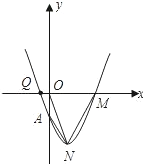（附加题）已知抛物线y=x2+kx+b经过点P（2，-3），Q（-1，0）．
若一次函数y=kx+b的图象如图所示，则抛物线y=x2+kx+b的对称轴位于y轴的