题目内容
 如图,已知AB⊥BD,CD⊥BD,点P在BD上,要使△ABP∽△PDC,可再添加的条件是________.
如图,已知AB⊥BD,CD⊥BD,点P在BD上,要使△ABP∽△PDC,可再添加的条件是________.
∠APB=∠PCD或∠PAB=∠CPD或 =
=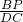
分析:已知两个三角形的两个对应角∠B=∠D=90°.若由“两角法”判定它们相似时,只需添加另一组对应角相等即可;若由“两边及其夹角法”判定它们相似时,只需添加 =
=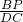 .
.
解答:如图,∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°.
∴只需添加∠APB=∠PCD或∠PAB=∠CPD或 =
=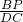 ,即可推知△ABP∽△PDC.
,即可推知△ABP∽△PDC.
故答案是:∠APB=∠PCD或∠PAB=∠CPD或 =
=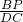 .
.
点评:本题考查了相似三角形的判定.此题为开放性试题,首先要找出已经满足的条件,然后再进一步分析需要添加的条件.
 =
=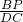
分析:已知两个三角形的两个对应角∠B=∠D=90°.若由“两角法”判定它们相似时,只需添加另一组对应角相等即可;若由“两边及其夹角法”判定它们相似时,只需添加
 =
=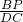 .
.解答:如图,∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°.
∴只需添加∠APB=∠PCD或∠PAB=∠CPD或
 =
=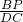 ,即可推知△ABP∽△PDC.
,即可推知△ABP∽△PDC.故答案是:∠APB=∠PCD或∠PAB=∠CPD或
 =
=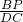 .
.点评:本题考查了相似三角形的判定.此题为开放性试题,首先要找出已经满足的条件,然后再进一步分析需要添加的条件.

练习册系列答案
相关题目
 9、如图,已知AB⊥BD,ED⊥BD,C是BD上一点,AB=CD,BC=ED,那么下列结论中,不正确的是( )
9、如图,已知AB⊥BD,ED⊥BD,C是BD上一点,AB=CD,BC=ED,那么下列结论中,不正确的是( ) 49、如图,已知AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,则∠ACE=
49、如图,已知AB⊥BD,垂足为B,ED⊥BD,垂足为D,AB=CD,BC=DE,则∠ACE=
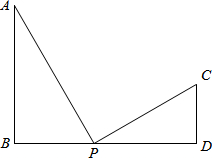 (2013•永州)如图,已知AB⊥BD,CD⊥BD
(2013•永州)如图,已知AB⊥BD,CD⊥BD 如图,已知AB⊥BD,BC⊥CD,AD=a,CD=b,则BD的长的取值范围为( )
如图,已知AB⊥BD,BC⊥CD,AD=a,CD=b,则BD的长的取值范围为( )