题目内容
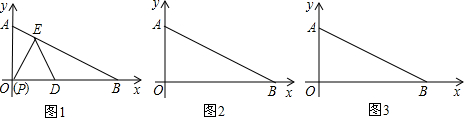
如图1,在Rt△AOB中,∠AOB=90°,∠ABO=30°,OB=4,以O点为原点,OB边所在直线为x轴,建立直角坐标系.在x轴上取一点D(2,0),作一个边长为2的等边△PDE,此时P点与O点重合,E点在线段AB上(如图).将△PDE沿x轴向右平移,直线AB与直线ED交于点F,回答下列问题:(1)找出一条与OP始终相等的线段,并说明理由;
(2)设点P与原点的距离为x,此时等边△PDE与Rt△AOB重叠部分的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.(图2,图3为备用图)
分析:(1)设出E点的坐标,从而表示出点P、F的坐标,求出线段EF的长度恰好等于OP;
(2)0≤x≤2时,设PE交AB于G,证明得出△GFE为直角三角形,又因为OP=EF,从而求出S△GFE,阴影部分面积即为S△EPD-S△GFE;2<x≤4时,重叠部分为直角△PGB的面积,由OP=x,得到PB=4-x,根据30°角所对的直角边等于斜边的一半求出PG的长,再利用30°的余弦函数值求出GB的长,利用直角边乘积的一半即可求出面积;x>4时△EFG在△AOB之外,y=0.
(2)0≤x≤2时,设PE交AB于G,证明得出△GFE为直角三角形,又因为OP=EF,从而求出S△GFE,阴影部分面积即为S△EPD-S△GFE;2<x≤4时,重叠部分为直角△PGB的面积,由OP=x,得到PB=4-x,根据30°角所对的直角边等于斜边的一半求出PG的长,再利用30°的余弦函数值求出GB的长,利用直角边乘积的一半即可求出面积;x>4时△EFG在△AOB之外,y=0.
解答: 解:(1)与OP始终相等的线段为EF,
解:(1)与OP始终相等的线段为EF,
证明:设等边△PDE运动到某位置时E点坐标为(x1,
)(x1≥1),
则P(x1-1,0),则OP=x1-1,
∵∠EDP=60°,E(x1,
)在直线ED上,
∴ED的解析式为y=-
(x-x1)+
,
由题意可得直线AB的解析式为y=-
x+
,
则直线AB和直线ED的交点F的坐标为(
,-
),
则EF=
=x1-1=OP,
∴与OP始终相等的线段为EF;
(2)设PE交AB与点G,由题意可知△PDE的面积为
,
当0≤x≤2时,在图1中∠EPB+∠GBP=60°+30°=90°,
∴PE⊥AB,
∴△EFG为直角三角形,
∵∠E=60°,EF=OP=x,
∴∠EFG=30°,
∴GE=
x,GF=
x,
∴S△EFG=
×EG×GF=
×
x×
x=
x2,
∴等边△PDE与Rt△AOB重叠部分的面积y=S△EPD-S△GFE,即y=
-
x(0≤x≤2);
当2<x≤4时,等边△PDE与Rt△AOB重叠部分的面积为S△PGB,
OP=x,则PB=4-x,所以PG=
,GB=
,且△PGB为直角三角形,
所以S△PGB=
×
×
=
;
当x>4时,两个三角形相离,故y=0.
 解:(1)与OP始终相等的线段为EF,
解:(1)与OP始终相等的线段为EF,证明:设等边△PDE运动到某位置时E点坐标为(x1,
| 3 |
则P(x1-1,0),则OP=x1-1,
∵∠EDP=60°,E(x1,
| 3 |
∴ED的解析式为y=-
| 3 |
| 3 |
由题意可得直线AB的解析式为y=-
| ||
| 3 |
4
| ||
| 3 |
则直线AB和直线ED的交点F的坐标为(
| 3x1-1 |
| 2 |
| ||||
| 2 |
则EF=
(x1-
|
∴与OP始终相等的线段为EF;
(2)设PE交AB与点G,由题意可知△PDE的面积为
| 3 |

当0≤x≤2时,在图1中∠EPB+∠GBP=60°+30°=90°,
∴PE⊥AB,
∴△EFG为直角三角形,
∵∠E=60°,EF=OP=x,
∴∠EFG=30°,
∴GE=
| 1 |
| 2 |
| ||
| 2 |
∴S△EFG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 8 |
∴等边△PDE与Rt△AOB重叠部分的面积y=S△EPD-S△GFE,即y=
| 3 |
| ||
| 8 |
当2<x≤4时,等边△PDE与Rt△AOB重叠部分的面积为S△PGB,
OP=x,则PB=4-x,所以PG=
| 4-x |
| 2 |
| ||
| 2 |
所以S△PGB=
| 1 |
| 2 |
| 4-x |
| 2 |
| ||
| 2 |
| ||
| 8 |
当x>4时,两个三角形相离,故y=0.
点评:本题考查了正三角形直角三角形面积求法及分类讨论的思想,具有较强的综合性.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
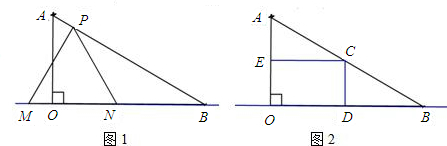

 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
 ,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒
,∠ABO=30°.动点P在线段AB上从点A向终点B以每秒 个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在直线OB 上取两点M、N作等边△PMN.