��Ŀ����
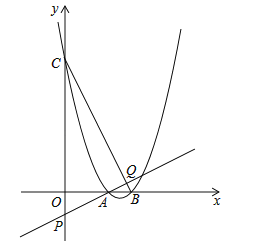
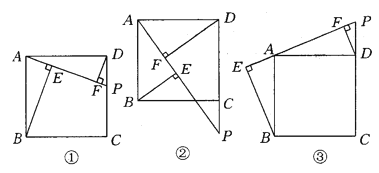
����Ŀ����ͼ1����֪������![]() ��ͼ����
��ͼ����![]() ��
��![]() ����Գ���Ϊֱ��
����Գ���Ϊֱ��![]() ������
������![]() ��
��![]() �ύ�������ڵ�
�ύ�������ڵ�![]() ��
��![]() ��ƽ���߽��߶�
��ƽ���߽��߶�![]() �ڵ�
�ڵ�![]() ����
����![]() ���������ϵ�һ�����㣬���������Ϊ
���������ϵ�һ�����㣬���������Ϊ![]() ��
��
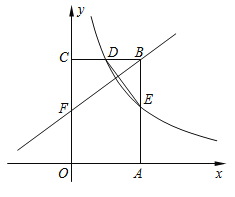
��1���������ߵĽ���ʽ��
��2��������![]() ��
��![]() ��
��![]() ����������ϣ�����
����������ϣ�����![]() ��
��![]() �����ı���
�����ı���![]() ���
���![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
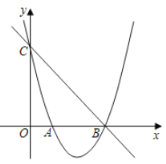
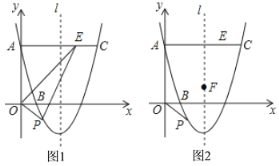
��3����ͼ2��![]() �������ߵĶԳ����ϵ�һ�㣬�ڶԳ����������������Ƿ���ڵ�
�������ߵĶԳ����ϵ�һ�㣬�ڶԳ����������������Ƿ���ڵ�![]() ʹ
ʹ![]() ��Ϊ�Ե�
��Ϊ�Ե�![]() Ϊֱ�Ƕ���ĵ���ֱ�������Σ������ڣ�ֱ��д�����з��������ĵ�
Ϊֱ�Ƕ���ĵ���ֱ�������Σ������ڣ�ֱ��д�����з��������ĵ�![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3����
����3����![]() ������Ϊ
������Ϊ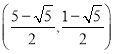 ��
��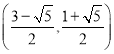 ��
��
��������
��1�����ȸ��ݶԳ��Եó���������![]() �����һ���������꣬Ȼ������������������߽���ʽ�������A�����꣬���ɵý⣻
�����һ���������꣬Ȼ������������������߽���ʽ�������A�����꣬���ɵý⣻
��2��������![]() �����ݽ�ƽ���ߵ����ʵó���AOE�ǵ���ֱ�������Σ�Ȼ���ı��ηֳ�������������⼴�ɵó�������ϵʽ��
�����ݽ�ƽ���ߵ����ʵó���AOE�ǵ���ֱ�������Σ�Ȼ���ı��ηֳ�������������⼴�ɵó�������ϵʽ��
��3�����������������ͼ��ʾ���������߹���ȫ�������Σ�����![]() ���з��̼��ɵó���P������.
���з��̼��ɵó���P������.
��1����ͼ������������![]() �����һ������Ϊ
�����һ������Ϊ![]()
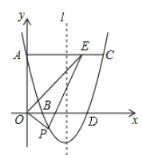
�ɶԳ��Եã�![]()
�������ߵĽ���ʽΪ��![]()
��![]() ����ã�
����ã�![]()
![]()
![]() �����ߵĽ���ʽ��
�����ߵĽ���ʽ��![]()
��2����ͼ����![]()
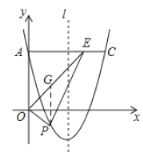
![]() ƽ��
ƽ��![]() ��
��![]()
![]()
![]() �ǵ���ֱ��������
�ǵ���ֱ��������
![]()
![]()
![]() ��
��
![]() ��
��
![]()
![]() ��
��
![]() ��
��
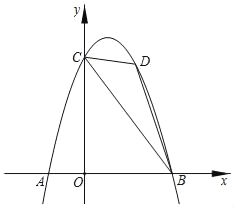
��3�������������
�ٵ�P��![]() ���·�ʱ������P��MN��
���·�ʱ������P��MN��![]() �ᣬ��
�ᣬ��![]() ����M�����Գ�����N����ͼ��ʾ��
����M�����Գ�����N����ͼ��ʾ��
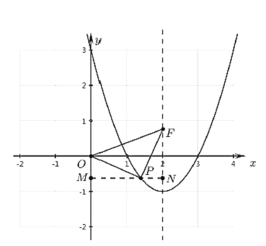
����POF�ǵ���ֱ�������Σ���OP=PF
����OMP�ա�PNF��
��OM=PN
��![]()
��![]()
���![]() ����ȥ����
����ȥ����![]()
���![]() ������Ϊ
������Ϊ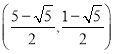
�ڵ�P��![]() ���Ϸ�ʱ����ͼ��ʾ��
���Ϸ�ʱ����ͼ��ʾ��
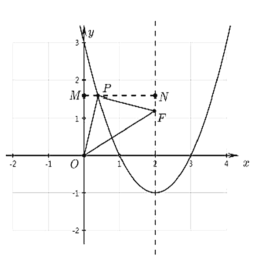
ͬ������![]()
���![]() ��
��![]() ����ȥ��
����ȥ��
���![]() ������Ϊ
������Ϊ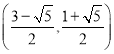
���ϣ���![]() ������Ϊ
������Ϊ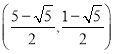 ��
��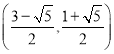 .
.

 ��У����ϵ�д�
��У����ϵ�д�