题目内容
20. 如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )| A. | 8cm | B. | $\sqrt{91}$cm | C. | 6cm | D. | 2cm |
分析 由于⊙O的直径CD=10cm,则⊙O的半径为5cm,又已知OM:OC=3:5,则可以求出OM=3,OC=5,连接OA,根据勾股定理和垂径定理可求得AB的长度.
解答 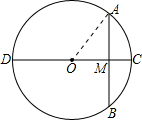 解:如图所示,连接OA.
解:如图所示,连接OA.
⊙O的直径CD=10cm,
则⊙O的半径为5cm,
即OA=OC=5,
又∵OM:OC=3:5,
所以OM=3,
∵AB⊥CD,垂足为M,
∴AM=BM,
在Rt△AOM中,AM=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AB=2AM=2×4=8.
故选A.
点评 此题考查了垂径定理,以及勾股定理,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
11.若代数式-$\sqrt{x+3}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥-3 | B. | x>3 | C. | x≥3 | D. | x≤3 |
8.在平面直角坐标系中,将点A(-1,1)向右平移5个单位长度得到点B,则点B关于y轴的对称点C的坐标是( )
| A. | (4,1) | B. | (4,-1) | C. | (-4,-1) | D. | (-4,1) |
15. 甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )
甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )
 甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )
甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为P,羽毛球距地面高度h(米)与其飞行的水平距离s(米)之间的关系式为h=-$\frac{1}{12}$s2+$\frac{2}{3}$s+$\frac{3}{2}$.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为$\frac{9}{4}$米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是( )| A. | 4<m<8+$\sqrt{7}$ | B. | 4-$\sqrt{7}$<m<5 | C. | 5<m<9 | D. | 5<m<4+$\sqrt{7}$ |
5.平面直角坐标系中,P(3,-2),则点P关于y轴对称的点的坐标为( )
| A. | (3,2) | B. | (-3,2) | C. | (-3,-2) | D. | (-2,-3) |
12.要使分式有$\frac{x}{x-1}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x<1 | D. | x≠-1 |
10.下列说法正确的是( )
| A. | 有理数的绝对值一定是正数 | |
| B. | 有理数的绝对值一定是非负数 | |
| C. | 绝对值等于本身的数一定是正数 | |
| D. | 如果两个数的绝对值相等,那么这两个数相等 |
 如图,直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
如图,直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )



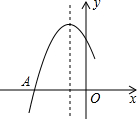 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论: