题目内容
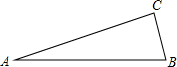 (2011•南宁)如图,在△ABC中,∠ACB=90°,∠A=15°,AB=8,则AC•BC的值为( )
(2011•南宁)如图,在△ABC中,∠ACB=90°,∠A=15°,AB=8,则AC•BC的值为( )分析:解法一:利用二倍角公式sin2α=2sinαcosα、锐角三角函数的定义解答.
解法二:作△ABC的中线CD,过C作CE⊥AB于E,求出AD=CD=BD=2,求出CE、DE、BE,根据勾股定理求出BC、AC,代入求出即可.
解法二:作△ABC的中线CD,过C作CE⊥AB于E,求出AD=CD=BD=2,求出CE、DE、BE,根据勾股定理求出BC、AC,代入求出即可.
解答:解:∵sin30°=2sin15°cos15°=
,∠A=15°,
∴2×
×
=
;
又∵AB=8,
∴AC•BC=16.
解法二:
作△ABC的中线CD,过C作CE⊥AB于E,
∵∠ACB=90°,
∴AD=DC=DB=
AB=4,
∴∠A=∠ACD=15°,
∴∠CDB=∠A+∠ACD=30°,
∴CE=
CD=2,
∴S△ABC=
AC•BC=
AB•CE,即
AC•BC=
×8×2,
∴AC•BC=16
故选D.
| 1 |
| 2 |
∴2×
| BC |
| AB |
| AC |
| AB |
| 1 |
| 2 |
又∵AB=8,
∴AC•BC=16.
解法二:

作△ABC的中线CD,过C作CE⊥AB于E,
∵∠ACB=90°,
∴AD=DC=DB=
| 1 |
| 2 |
∴∠A=∠ACD=15°,
∴∠CDB=∠A+∠ACD=30°,
∴CE=
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AC•BC=16
故选D.
点评:本题考查了锐角三角函数的定义.解答该题的关键是熟记二倍角公式.

练习册系列答案
相关题目
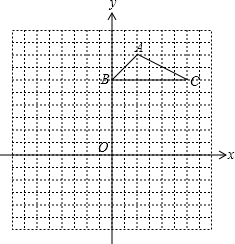 (2011•南宁)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(2011•南宁)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系. 于点B.
于点B. (2011•南宁)如图,三视图描述的实物形状是( )
(2011•南宁)如图,三视图描述的实物形状是( ) (2011•南宁)如图,在圆锥形的稻草堆顶点P处有一只猫,看到底面圆周上的点A处有一只老鼠,猫沿着母线PA下去抓老鼠,猫到达点A时,老鼠已沿着底面圆周逃跑,猫在后面沿着相同的路线追,在圆周的点B处抓到了老鼠后沿母线BP回到顶点P处.在这个过程中,假设猫的速度是匀速的,猫出发后与点P距离s,所用时间为t,则s与t之间的函数关系图象是( )
(2011•南宁)如图,在圆锥形的稻草堆顶点P处有一只猫,看到底面圆周上的点A处有一只老鼠,猫沿着母线PA下去抓老鼠,猫到达点A时,老鼠已沿着底面圆周逃跑,猫在后面沿着相同的路线追,在圆周的点B处抓到了老鼠后沿母线BP回到顶点P处.在这个过程中,假设猫的速度是匀速的,猫出发后与点P距离s,所用时间为t,则s与t之间的函数关系图象是( )