题目内容
用一个半径为8，圆心角为90°的扇形围成一个圆锥的侧面，则圆锥的高为________．
2
分析：根据扇形的半径为8，圆心角为90°，可以得出扇形的面积S=
，根据圆锥的侧面积公式：S=πRL，这两部分相等，从而可求出R，已知扇形的半径为8，正好是圆锥的母线长，再利用勾股定理可以求出圆锥的高．
解答：∵扇形的半径为8，圆心角为90°，
∴扇形的面积S==
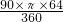=16π，
根据圆锥的侧面积公式：S=πRL，
∴πRL=16π，
8πR=16π，
∴R=2，
∴圆锥的高为：
=2，
故答案为：2．
点评：此题主要考查了圆锥侧面展开图与扇形的各部分对应情况，求出圆锥的底面圆的半径是解决问题的关键．
分析：根据扇形的半径为8，圆心角为90°，可以得出扇形的面积S=
，根据圆锥的侧面积公式：S=πRL，这两部分相等，从而可求出R，已知扇形的半径为8，正好是圆锥的母线长，再利用勾股定理可以求出圆锥的高．解答：∵扇形的半径为8，圆心角为90°，
∴扇形的面积S=
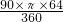==16π，根据圆锥的侧面积公式：S=πRL，
∴πRL=16π，
8πR=16π，
∴R=2，
∴圆锥的高为：
=2，故答案为：2
．点评：此题主要考查了圆锥侧面展开图与扇形的各部分对应情况，求出圆锥的底面圆的半径是解决问题的关键．
练习册系列答案
相关题目
