题目内容
【题目】如图,点![]() 为
为![]() 轴负半轴上的一个点,过点
轴负半轴上的一个点,过点![]() 作
作![]() 轴的垂线,交函数
轴的垂线,交函数![]() 的图像于点
的图像于点![]() ,交函数
,交函数![]() 的图像于点
的图像于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() ,连接
,连接![]() .
.
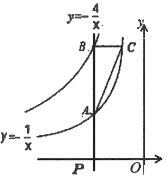
(1)当点![]() 的坐标为(–1,0)时,求
的坐标为(–1,0)时,求![]() 的面积;
的面积;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)连接![]() 和
和![]() .当点
.当点![]() 的坐标为(
的坐标为(![]() ,0)时,
,0)时,![]() 的面积是否随
的面积是否随![]() 的值的变化而变化?请说明理由.
的值的变化而变化?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的面积不随t的值的变化而变化,理由见解析。
的面积不随t的值的变化而变化,理由见解析。
【解析】
(1)根据题意首先计算出C点的坐标,再计算三角形的面积.
(2)首先利用反比例函数的关系式设出A点的坐标,在表示B、C点的坐标,结合AB=BC求解未知数,即可的A点的坐标.
(3)过点C作![]() 轴于点E,
轴于点E,![]() 轴于点D,再根据P点的坐标表示A、B、C点的坐标,再利用
轴于点D,再根据P点的坐标表示A、B、C点的坐标,再利用![]() ,即可求解出
,即可求解出![]() 的面积.
的面积.
解:(1)当点P的坐标为![]() 时,点A、B的横坐标为-1,
时,点A、B的横坐标为-1,
∵点A在反比例函数![]() 上,点B在反比例函数
上,点B在反比例函数![]() 上,
上,
∴点![]() ,点
,点![]() .
.
![]() 轴,
轴,
∴点C的纵坐标为4,
又∵点C在![]() 上,∴点C的坐标为
上,∴点C的坐标为![]() ,
,
![]()
(2)设点A的坐标为![]() ,则
,则![]()
则![]()
得方程![]() ,解之,得
,解之,得![]() (含正),
(含正),
![]()
(3)过点C作![]() 轴于点E,
轴于点E,![]() 轴于点D。如图所示:
轴于点D。如图所示:
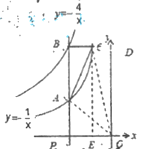
∵点P的坐标为![]() ,
,
∴点A的坐标为![]() ,点
,点![]() ,点
,点![]()
![]()
故![]() 的面积不随t的值的变化而变化
的面积不随t的值的变化而变化

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目