题目内容
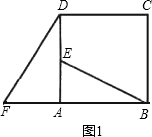
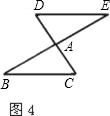
阅读下列材料:如图1,在梯形ABCD中,AD∥BC,点M,N分别在边AB,DC上,且MN∥AD,记AD=a,BC=b.若
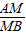 =
=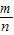 ,则有结论:MN=
,则有结论:MN=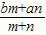 .
.请根据以上结论,解答下列问题:
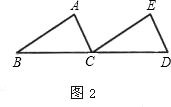
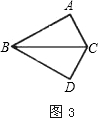
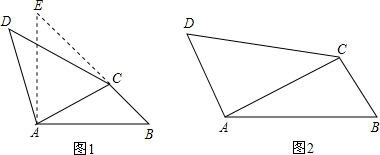
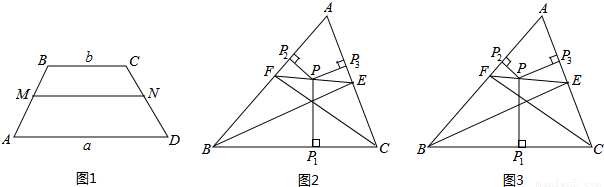
如图2,图3,BE,CF是△ABC的两条角平分线,过EF上一点P分别作△ABC三边的垂线段PP1,PP2,PP3,交BC于点P1,交AB于点P2,交AC于点P3.
(1)若点P为线段EF的中点.求证:PP1=PP2+PP3;
(2)若点P为线段EF上的任意位置时,试探究PP1,PP2,PP3的数量关系,并给出证明.
【答案】分析:(1)如答图1所示,作辅助线,由角平分线性质可知ER=ES,FM=FN;再由中位线性质得到FM=2PP3,ER=2PP2;最后,在梯形FMRE中,援引题设结论,列出关系式,化简得到:PP1=PP2+PP3;
(2)如答图2所示,作辅助线,由角平分线性质可知ER=ES,FM=FN;再由相似三角形比例线段关系得到:ER= PP2;FM=
PP2;FM=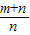 PP3;最后,在梯形FMRE中,援引题设结论,列出关系式,化简得到:PP1=PP2+PP3.
PP3;最后,在梯形FMRE中,援引题设结论,列出关系式,化简得到:PP1=PP2+PP3.
解答:(1)证明:如答图1所示,
BE为角平分线,过点E作ER⊥BC于点R,ES⊥AB于点S,则有ER=ES;
CF为角平分线,过点F作FM⊥BC于点M,FN⊥AC于点N,则有FM=FN.

点P为中点,由中位线的性质可知:ES=2PP2,FN=2PP3.
∴FM=2PP3,ER=2PP2.
在梯形FMRE中,FM∥PP1∥ER, ,
,
根据题设结论可知:
PP1= =
= =
= =PP2+PP3.
=PP2+PP3.
∴PP1=PP2+PP3.
(2)探究结论:PP1=PP2+PP3.
证明:如答图2所示,
BE为角平分线,过点E作ER⊥BC于点R,ES⊥AB于点S,则有ER=ES;
CF为角平分线,过点F作FM⊥BC于点M,FN⊥AC于点N,则有FM=FN.

点P为EF上任意一点,不妨设 ,则
,则 ,
, .
.
∵PP2∥ES,∴ =
= ,∴ES=
,∴ES= PP2;
PP2;
∵PP3∥FN,∴ ,∴FN=
,∴FN= PP3.
PP3.
∴ER= PP2;FM=
PP2;FM= PP3.
PP3.
在梯形FMRE中,FM∥PP1∥ER, ,
,
根据题设结论可知:
PP1= =
= =
= =PP2+PP3.
=PP2+PP3.
∴PP1=PP2+PP3.
点评:本题是几何综合题,考查了相似三角形的判定与性质、角平分线的性质.本题两问之间体现了由特殊到一般的数学思想,解题思路类似,并且同学们可仔细领会.
(2)如答图2所示,作辅助线,由角平分线性质可知ER=ES,FM=FN;再由相似三角形比例线段关系得到:ER=
 PP2;FM=
PP2;FM=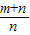 PP3;最后,在梯形FMRE中,援引题设结论,列出关系式,化简得到:PP1=PP2+PP3.
PP3;最后,在梯形FMRE中,援引题设结论,列出关系式,化简得到:PP1=PP2+PP3.解答:(1)证明:如答图1所示,
BE为角平分线,过点E作ER⊥BC于点R,ES⊥AB于点S,则有ER=ES;
CF为角平分线,过点F作FM⊥BC于点M,FN⊥AC于点N,则有FM=FN.

点P为中点,由中位线的性质可知:ES=2PP2,FN=2PP3.
∴FM=2PP3,ER=2PP2.
在梯形FMRE中,FM∥PP1∥ER,
 ,
,根据题设结论可知:
PP1=
 =
= =
= =PP2+PP3.
=PP2+PP3.∴PP1=PP2+PP3.
(2)探究结论:PP1=PP2+PP3.
证明:如答图2所示,
BE为角平分线,过点E作ER⊥BC于点R,ES⊥AB于点S,则有ER=ES;
CF为角平分线,过点F作FM⊥BC于点M,FN⊥AC于点N,则有FM=FN.

点P为EF上任意一点,不妨设
 ,则
,则 ,
, .
.∵PP2∥ES,∴
 =
= ,∴ES=
,∴ES= PP2;
PP2;∵PP3∥FN,∴
 ,∴FN=
,∴FN= PP3.
PP3.∴ER=
 PP2;FM=
PP2;FM= PP3.
PP3.在梯形FMRE中,FM∥PP1∥ER,
 ,
,根据题设结论可知:
PP1=
 =
= =
= =PP2+PP3.
=PP2+PP3.∴PP1=PP2+PP3.
点评:本题是几何综合题,考查了相似三角形的判定与性质、角平分线的性质.本题两问之间体现了由特殊到一般的数学思想,解题思路类似,并且同学们可仔细领会.

练习册系列答案
相关题目
 阅读下列材料:
阅读下列材料: