题目内容
4. 在等边△ABC中,点E是边AB上一点,ED=EC
在等边△ABC中,点E是边AB上一点,ED=EC(1)求证:AE=BD;
(2)当EG=GC且AG=1.5时,求AD的长.
分析 (1)过E作EF∥BC交AC于F,求出等边三角形AEF,证△DEB和△ECF全等,求出BD=EF即可;
(2)过C作CH∥AB交AG的延长线于H,根据平行线的性质得到∠EAG=∠H,∠ABC=∠BCH=60°,推出△AEG≌△CGH,根据全等三角形的性质得到AE=CH,AG=GH=1.5,由(1)知BD=AE,证得△ABD≌△ACH,根据全等三角形的性质即可得到结论.
解答 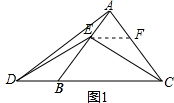 (1)证明:如图1,过点E作EF∥BC交AC于点F,如图1所示:
(1)证明:如图1,过点E作EF∥BC交AC于点F,如图1所示:
∴∠AEF=∠ABC,∠AFE=∠ACB,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,AB=AC=BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,
即∠AEF=∠AFE=∠EAF=60°,
∴△AEF是等边三角形,
∴∠DBE=∠EFC=120°,∠EDB+∠BED=∠FCE+∠ECD=60°,
∵DE=EC,
∴∠EDB=∠ECD,
∴∠BED=∠ECF,
在△DEB和△ECF中,$\left\{\begin{array}{l}{∠DEB=∠ECF}\\{∠DBE=∠EFC}\\{DE=EC}\end{array}\right.$,
∴△DEB≌△ECF(AAS),
∴DB=EF,
∴AE=BD;
(2)如图2,过C作CH∥AB交AG的延长线于H,
∴∠EAG=∠H,∠ABC=∠BCH=60°,
在△AEG与△HCG中,$\left\{\begin{array}{l}{∠EAG=∠H}\\{∠AGE=∠CGH}\\{EG=CG}\end{array}\right.$,
∴△AEG≌△CGH,
∴AE=CH,AG=GH=1.5,
由(1)知BD=AE,
∴BD=CH,
∵∠ABD=∠ACH=120°,
在△ADB与△AHC中,$\left\{\begin{array}{l}{AB=AC}\\{∠ABD=∠ACH}\\{BD=CH}\end{array}\right.$,
∴△ABD≌△ACH,
∴AD=AH=2AG=3.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,平行线的性质,正确的作出辅助线是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | y=-3(x-1)2-3 | B. | y=-3(x-1)2-1 | C. | y=-3(x=1)2-3 | D. | y=-3(x+1)2-1 |
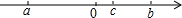 a,b,c在数轴上的位置如图所示,求|c-b|-$\sqrt{(a+b)^{2}}$-$\root{3}{(a+c)^{3}}$的值.
a,b,c在数轴上的位置如图所示,求|c-b|-$\sqrt{(a+b)^{2}}$-$\root{3}{(a+c)^{3}}$的值.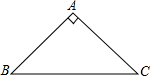 如图,在△ABC中,AB=AC,∠BAC=90°,点D为射线CB上一点,连接AD,以AD为一边在AD右侧作正方形ADEF,直线EF与直线BC交于点M,若AB=2$\sqrt{2}$,BD=1,则CM的长为$\frac{1}{2}$或$\frac{3}{2}$.
如图,在△ABC中,AB=AC,∠BAC=90°,点D为射线CB上一点,连接AD,以AD为一边在AD右侧作正方形ADEF,直线EF与直线BC交于点M,若AB=2$\sqrt{2}$,BD=1,则CM的长为$\frac{1}{2}$或$\frac{3}{2}$. 如图,四边形ABCD中,AC平分∠BAD,∠ADC+∠ABC=180°,CE⊥AB于E,猜想AD、AE、AB之间的关系式,并证明你的猜想.
如图,四边形ABCD中,AC平分∠BAD,∠ADC+∠ABC=180°,CE⊥AB于E,猜想AD、AE、AB之间的关系式,并证明你的猜想. 如图所示,抛物线y=x2-4x+3与x轴分别交于A、B两点,交y轴于点C,
如图所示,抛物线y=x2-4x+3与x轴分别交于A、B两点,交y轴于点C,