题目内容
我们学习过二次函数的图象的平移,先作出二次函数y=2x2+1的图象.①向上平移3个单位,所得图象的函数表达式是
②向下平移4个单位,所得图象的函数表达式是
③向左平移5个单位,所得图象的函数表达式是
④向右平移6个单位,所得图象的函数表达式是
由此可以归纳二次函数y=ax2+c向上平移m个单位,所得图象的函数表达式是
我们来研究二次函数的图象的翻折,在一张纸上作出二次函数y=x2-2x-3的图象,
⑤沿x轴把这张纸对折,所得图象的函数表达式是
⑥沿y轴把这张纸对折,所得图象的函数表达式是
由此可以归纳二次函数y=ax2+bx+c若沿x轴翻折,所得图象的函数表达式是
我们继续研究二次函数的图象的旋转,将二次函数y=-
| 1 | 2 |
由此可以归纳二次函数y=ax2+bx+c的图象绕原点旋转180°,所得图象的函数表达式是
分析:①向上平移,顶点的纵坐标1+3即可;
②向下平移,顶点的纵坐标1-4即可;
③向左平移,顶点的横坐标0-5即可;
④向右平移,顶点的横坐标0+6即可;
⑤两抛物线关于x轴对称,那么二次项的系数,一次项的系数,常数项均互为相反数;
⑥两抛物线关于y轴对称,二次项系数,常数项不变,一次项系数互为相反数;绕原点旋转180°可得实际是两抛物线关于x轴对称.
②向下平移,顶点的纵坐标1-4即可;
③向左平移,顶点的横坐标0-5即可;
④向右平移,顶点的横坐标0+6即可;
⑤两抛物线关于x轴对称,那么二次项的系数,一次项的系数,常数项均互为相反数;
⑥两抛物线关于y轴对称,二次项系数,常数项不变,一次项系数互为相反数;绕原点旋转180°可得实际是两抛物线关于x轴对称.
解答:解:①y=2x2+4;
②y=2x2-3;
③y=2(x+5)2+1;
④y=2(x-6)2+1;
y=ax2+c+m;y=ax2+c-m;y=a(x+n)2+c;y=a(x-n)2+c;
⑤y=-x2+2x+3;
⑥y=x2+2x-3 y=-ax2-bx-c;y=ax2-bx+c;y=
x2-x+1;y=-ax2-bx-c.
②y=2x2-3;
③y=2(x+5)2+1;
④y=2(x-6)2+1;
y=ax2+c+m;y=ax2+c-m;y=a(x+n)2+c;y=a(x-n)2+c;
⑤y=-x2+2x+3;
⑥y=x2+2x-3 y=-ax2-bx-c;y=ax2-bx+c;y=
| 1 |
| 2 |
点评:本题考查二次函数的变化特点,需注意动手操作,观察得到相应规律.

练习册系列答案
相关题目
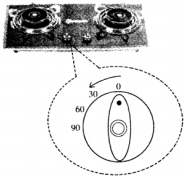 (2012•潍坊)许多家庭以燃气作为烧水做饭的燃料,节约用气是我们日常生活中非常现实的问题.某款燃气灶旋转位置从0度到90度(如图),燃气关闭时,燃气灶旋转的位置为0度,旋转角度越大,燃气流量越大,燃气开到最大时,旋转角度为90度.为测试燃气灶旋转在不同位置上的燃气用量,在相同条件下,选择燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时,其火力不能够将水烧开,故选择旋钮角度x度的范围是18≤x≤90),记录相关数据得到下表:
(2012•潍坊)许多家庭以燃气作为烧水做饭的燃料,节约用气是我们日常生活中非常现实的问题.某款燃气灶旋转位置从0度到90度(如图),燃气关闭时,燃气灶旋转的位置为0度,旋转角度越大,燃气流量越大,燃气开到最大时,旋转角度为90度.为测试燃气灶旋转在不同位置上的燃气用量,在相同条件下,选择燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时,其火力不能够将水烧开,故选择旋钮角度x度的范围是18≤x≤90),记录相关数据得到下表: +x-1的图象,绕原点旋转180°,所得图象的函数表达式是________;
+x-1的图象,绕原点旋转180°,所得图象的函数表达式是________;
 +x-1的图象,绕原点旋转180°,所得图象的函数表达式是______;
+x-1的图象,绕原点旋转180°,所得图象的函数表达式是______;