题目内容
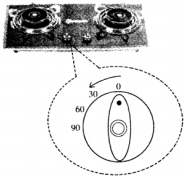 (2012•潍坊)许多家庭以燃气作为烧水做饭的燃料,节约用气是我们日常生活中非常现实的问题.某款燃气灶旋转位置从0度到90度(如图),燃气关闭时,燃气灶旋转的位置为0度,旋转角度越大,燃气流量越大,燃气开到最大时,旋转角度为90度.为测试燃气灶旋转在不同位置上的燃气用量,在相同条件下,选择燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时,其火力不能够将水烧开,故选择旋钮角度x度的范围是18≤x≤90),记录相关数据得到下表:
(2012•潍坊)许多家庭以燃气作为烧水做饭的燃料,节约用气是我们日常生活中非常现实的问题.某款燃气灶旋转位置从0度到90度(如图),燃气关闭时,燃气灶旋转的位置为0度,旋转角度越大,燃气流量越大,燃气开到最大时,旋转角度为90度.为测试燃气灶旋转在不同位置上的燃气用量,在相同条件下,选择燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时,其火力不能够将水烧开,故选择旋钮角度x度的范围是18≤x≤90),记录相关数据得到下表:| 旋钮角度(度) | 20 | 50 | 70 | 80 | 90 |
| 所用燃气量(升) | 73 | 67 | 83 | 97 | 115 |
(2)当旋钮角度为多少时,烧开一壶水所用燃气量最少?最少是多少?
(3)某家庭使用此款燃气灶,以前习惯把燃气开到最大,现采用最节省燃气的旋钮角度,每月平均能节约燃气10立方米,求该家庭以前每月的平均燃气量.
分析:(1)先假设函数为一次函数,任选两点求出函数解析式,再将各点代入验证;再假设函数为二次函数,任选三求出函数解析式,再将各点代入验证
(2)将(1)所求二次函数解析式,化为顶点式,转化为二次函数最值的问题,即可解答.
(3)由(2)及表格知,采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115-65=50,再设该家庭以前每月平均用气量为a立方米,据此解答即可.
(2)将(1)所求二次函数解析式,化为顶点式,转化为二次函数最值的问题,即可解答.
(3)由(2)及表格知,采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115-65=50,再设该家庭以前每月平均用气量为a立方米,据此解答即可.
解答:解:(1)若设y=kx+b(k≠0),
由
,
解得
,
所以y=-
x+77,把x=70代入得y=63≠83,所以不符合;
若设y=
(k≠0),由73=
,解得k=1460,
所以y=
,把x=50代入得y=29.2≠67,所以不符合;
若设y=ax2+bx+c,
则由
,
解得
,
所以y=
x2-
x+97(18≤x≤90),
把x=80代入得y=97,把x=90代入得y=115,符合题意.
所以二次函数能表示所用燃气量y升与旋钮角度x度的变化规律;
(2)由(1)得:y=
x2-
x+97=
(x-40)2+65,
所以当x=40时,y取得最小值65.
即当旋钮角度为40°时,烧开一壶水所用燃气量最少,最少为65升;
(3)由(2)及表格知,采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115-65=50(升)
设该家庭以前每月平均用气量为a立方米,则由题意得:
a=10,
解得a=23(立方米),
即该家庭以前每月平均用气量为23立方米.
由
|
解得
|
所以y=-
| 1 |
| 5 |
若设y=
| k |
| x |
| k |
| 20 |
所以y=
| 1460 |
| x |
若设y=ax2+bx+c,
则由
|
解得
|
所以y=
| 1 |
| 50 |
| 8 |
| 5 |
把x=80代入得y=97,把x=90代入得y=115,符合题意.
所以二次函数能表示所用燃气量y升与旋钮角度x度的变化规律;
(2)由(1)得:y=
| 1 |
| 50 |
| 8 |
| 5 |
| 1 |
| 50 |
所以当x=40时,y取得最小值65.
即当旋钮角度为40°时,烧开一壶水所用燃气量最少,最少为65升;
(3)由(2)及表格知,采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一壶水节约用气115-65=50(升)
设该家庭以前每月平均用气量为a立方米,则由题意得:
| 50 |
| 115 |
解得a=23(立方米),
即该家庭以前每月平均用气量为23立方米.
点评:本题考查了待定系数法求二次函数解析式、二次函数求最值等问题,综合性较强,需要有较高的思维能力,关键是探索出函数的解析式.

练习册系列答案
相关题目
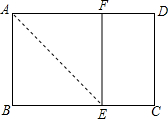 (2012•潍坊)已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( )
(2012•潍坊)已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( )