题目内容
6．观察如图的等式：
试一试：13+23+3 3+43+53=225．
想一想：13+23+3 3+43+…+n3=（1+2+3+4+…+n）2．
分析 通过观察和计算可知左边各项幂的底数的和等于右边幂的底数；由此规律并求得此式的值；进一步用式子表示即可．
解答 解：13+23+3 3+43+53=（1+2+3+4+5）2=225；
13+23+3 3+43+…+n3=（1+2+3+4+…+n）2．
故答案为：225；（1+2+3+4+…+n）2．
点评 此题主要考查了数字的变化规律，找等式的规律时，要注意观察等式的左边和右边的规律，还要注意观察等式的左右两边之间的关系．
练习册系列答案
相关题目
17．如果两条不同的直线都和第三条直线平行，那么这两条直线的位置关系是（ ）
| A． | 平行 | B． | 相交 | C． | 平行或相交 | D． | 互相垂直 |
1．一个多边形的各个内角都等于120°，则它的边数为（ ）
| A． | 3 | B． | 6 | C． | 7 | D． | 8 |
11．
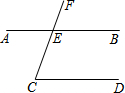如图，已知AB∥CD，CF交AB于点E，∠AEF=102°36′，则∠C等于（ ）
如图，已知AB∥CD，CF交AB于点E，∠AEF=102°36′，则∠C等于（ ）| A． | 77°24′ | B． | 78°24′ | C． | 78°36′ | D． | 102°36′ |
如图，在矩形ABCD中，AB=7cm，BC=$\sqrt{2}$cm，点P从点A出发以1cm/s的速度移动到点B．点P出发$\frac{28-2\sqrt{43}}{3}$秒后，PA=2PC．