题目内容
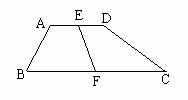
若AB∥CD，AD∥BC，则∠1+∠3+∠C=________．
180°
分析：由AB∥CD可得∠1=∠CDB，由AD∥BC可得∠C+∠ADC=180°，即可得∠1+∠3+∠C=180°．
解答：∵AB∥CD，
∴∠1=∠CDB（两直线平行，内错角相等），
∵AD∥BC，
∴∠C+∠ADC=180°（两直线平行，同旁内角互补），
∵∠ADC=∠3+∠CDB，
∴∠1+∠3+∠C=180°．
点评：本题考查了平行线的性质，正确找到相应关系的角是解题的关键．
分析：由AB∥CD可得∠1=∠CDB，由AD∥BC可得∠C+∠ADC=180°，即可得∠1+∠3+∠C=180°．
解答：∵AB∥CD，
∴∠1=∠CDB（两直线平行，内错角相等），
∵AD∥BC，
∴∠C+∠ADC=180°（两直线平行，同旁内角互补），
∵∠ADC=∠3+∠CDB，
∴∠1+∠3+∠C=180°．
点评：本题考查了平行线的性质，正确找到相应关系的角是解题的关键．
练习册系列答案
相关题目
20、若AB∥CD，AD∥BC，则∠1+∠3+∠C=
,AC=2
，BC=
(m>n>0).
,BC=
,(m>n>0).
(
)．