题目内容
已知方程2x2+4x-1=0的两根为x1和x2,则:
(1)x1+x2=______;
(2)x1x2=______;
(3) +
+ =______;
=______;
(4) +
+ =______;
=______;
(5)(x1-x2)2=______;
(6)(x1-2)(x2-2)=______;
(7)|x1-x2|=______.
解:(1)x1+x2=-2;
(2)x1x2=- ;
;
(3) +
+ =
=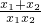 =
= =4;
=4;
(4) +
+ =
= =
= =-10;
=-10;
(5)(x1-x2)2=(x1+x2)2-2x1•x2=4+1=5;
(6)(x1-2)(x2-2)=x1•x2-2(x1+x2)+4=- +4+4=
+4+4= ;
;
(7)|x1-x2|= .
.
故答案为-2,- ,4,-10,5,
,4,-10,5, ,
, .
.
分析:(1)、(2)利用根与系数的关系直接求解;
(3)先通分得到 +
+ =
=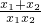 ,然后利用整体代入的方法计算;
,然后利用整体代入的方法计算;
(4)先通分,再利用完全平方公式变形得到 +
+ =
= ,然后利用整体代入的方法计算;
,然后利用整体代入的方法计算;
(5)先利用完全平方公式变形得到(x1-x2)2=(x1+x2)2-2x1•x2,然后利用整体代入的方法计算;
(6)先展开变形得到(x1-2)(x2-2)=x1•x2-2(x1+x2)+4,然后利用整体代入的方法计算;
(7)由(5)的计算结果和算术平方根的定义求解.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=- ,x1•x2=
,x1•x2= .
.
(2)x1x2=-
 ;
;(3)
 +
+ =
=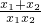 =
= =4;
=4;(4)
 +
+ =
= =
= =-10;
=-10;(5)(x1-x2)2=(x1+x2)2-2x1•x2=4+1=5;
(6)(x1-2)(x2-2)=x1•x2-2(x1+x2)+4=-
 +4+4=
+4+4= ;
;(7)|x1-x2|=
 .
.故答案为-2,-
 ,4,-10,5,
,4,-10,5, ,
, .
.分析:(1)、(2)利用根与系数的关系直接求解;
(3)先通分得到
 +
+ =
=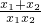 ,然后利用整体代入的方法计算;
,然后利用整体代入的方法计算;(4)先通分,再利用完全平方公式变形得到
 +
+ =
= ,然后利用整体代入的方法计算;
,然后利用整体代入的方法计算;(5)先利用完全平方公式变形得到(x1-x2)2=(x1+x2)2-2x1•x2,然后利用整体代入的方法计算;
(6)先展开变形得到(x1-2)(x2-2)=x1•x2-2(x1+x2)+4,然后利用整体代入的方法计算;
(7)由(5)的计算结果和算术平方根的定义求解.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
 ,x1•x2=
,x1•x2= .
. 
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目

