题目内容
已知:三角形纸片ABC中,∠C=90°,AB=12,BC=6,B′是边AC上一点.将三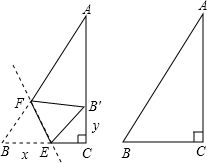 角形纸片折叠,使点B与点B′重合,折痕与BC、AB分别相交于E、F.
角形纸片折叠,使点B与点B′重合,折痕与BC、AB分别相交于E、F.(1)设BE=x,B′C=y,试建立y关于x的函数关系式,并直接写出x的取值范围;
(2)当△AFB′是直角三角形时,求出x的值.
分析:(1)根据折叠的性质得BE=B′E=x,在Rt△EB'C中利用勾股定理得y2+(6-x)2=x2,整理后即可得到y关于x的函数关系式;
(2)根据含30度的直角三角形三边的关系得∠A=30°,由折叠的性质得到∠FB'E=∠B=60°,然后讨论:①当∠AFB'=90°时,则∠AB′F=60°,易得∠B'EC=30°,
则B′C=
B′E,即y=
x,把y代入得到关于x的方程,解方程求出满足条件的x的值;②当∠AB'F=90°时,则∠EB'C=30°,即有EC=
EB′,即6-x=
x,解方程即可.
(2)根据含30度的直角三角形三边的关系得∠A=30°,由折叠的性质得到∠FB'E=∠B=60°,然后讨论:①当∠AFB'=90°时,则∠AB′F=60°,易得∠B'EC=30°,
则B′C=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵三角形纸片折叠,使点B与点B′重合,
∴BE=B′E,
∴B'E=x,CE=6-x,
在Rt△EB'C中,B'E2=CE2+B'C2,即y2+(6-x)2=x2,
∴y=
=2
(3≤x≤6);
(2)∵∠C=90°,AB=12,BC=6,
∴∠A=30°,
∴∠FB'E=∠B=60°,
①当∠AFB'=90°时,则∠AB′F=60°,
∴∠EB'C=60°,
∴∠B'EC=30°,
∴B′C=
B′E,即y=
x,
∴2
=
x,解得x=24±12
,
∵3≤x≤6,
∴x=24-12
;
②当∠AB'F=90°时,则∠EB'C=30°,
∴EC=
EB′,即6-x=
x,解得x=4,
所以x=4或24-12
时,△AFB’是直角三角形.
∴BE=B′E,
∴B'E=x,CE=6-x,
在Rt△EB'C中,B'E2=CE2+B'C2,即y2+(6-x)2=x2,
∴y=
| 12x-36 |
| 3x-9 |
(2)∵∠C=90°,AB=12,BC=6,
∴∠A=30°,
∴∠FB'E=∠B=60°,
①当∠AFB'=90°时,则∠AB′F=60°,
∴∠EB'C=60°,
∴∠B'EC=30°,
∴B′C=
| 1 |
| 2 |
| 1 |
| 2 |
∴2
| 3x-9 |
| 1 |
| 2 |
| 3 |
∵3≤x≤6,
∴x=24-12
| 3 |
②当∠AB'F=90°时,则∠EB'C=30°,
∴EC=
| 1 |
| 2 |
| 1 |
| 2 |
所以x=4或24-12
| 3 |
点评:本题考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应边相等.也考查了含30度的直角三角形三边的关系以及勾股定理.

练习册系列答案
相关题目
 A1MN与四边形BCNM重叠部分的面积为y,当x为何值时,y最大,最大值为多少.
A1MN与四边形BCNM重叠部分的面积为y,当x为何值时,y最大,最大值为多少.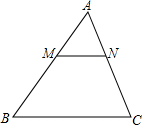 BCNM内的点A′,△A′MN与四边形BCNM重叠部分的面积为y.
BCNM内的点A′,△A′MN与四边形BCNM重叠部分的面积为y. 如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( ) 如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕翻折△ABC,使AB的一部分与BC重合,A与BC延长线上的点D重合,则线段AD的长度为( )
如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕翻折△ABC,使AB的一部分与BC重合,A与BC延长线上的点D重合,则线段AD的长度为( )