题目内容
等腰三角形一腰上的高与另一腰的夹角为35°,求这个三角形的各个内角的度数.
考点:等腰三角形的性质
专题:
分析:根据题意,一种情况为等腰三角形为锐角等腰三角形,根据垂直的性质外角的性质即可推出顶角为125°,另一种情况为等腰三角形为钝角三角形,根据三角形内角和定理和垂直的定理即可推出顶角为55°.
解答:解:①此等腰三角形为钝角三角形,
∵等腰三角形一腰上的高与另一腰的夹角为35°,
∴此三角形的顶角=90°+35°=125°,
∴等腰三角形的各角的度数为125°,37.5°,37.5°;
②此等腰三角形为锐角三角形,
∵等腰三角形一腰上的高与另一腰的夹角为35°,
∴此三角形的顶角=90°-35°=55°,
所以等腰三角形的各角的度数为55°,62.5°,62.5°.
∵等腰三角形一腰上的高与另一腰的夹角为35°,
∴此三角形的顶角=90°+35°=125°,
∴等腰三角形的各角的度数为125°,37.5°,37.5°;
②此等腰三角形为锐角三角形,
∵等腰三角形一腰上的高与另一腰的夹角为35°,
∴此三角形的顶角=90°-35°=55°,
所以等腰三角形的各角的度数为55°,62.5°,62.5°.
点评:本题主要考查外角的性质、三角形内角和定理,垂直的性质,关键在于根据题意分析讨论,认真的进行计算.

练习册系列答案
相关题目
下列各数中是无理数的是( )
| A、1.232232223 | |||
B、
| |||
C、
| |||
D、
|
下列是计算正确的是( )
| A、-8-3=-5 |
| B、-(-2)2=4 |
| C、-(x-y)=x+y |
| D、ab+2ba=3ab |
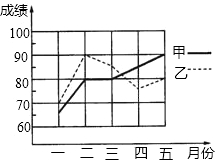 为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛,统计了他们从今年1到5月的每个月的一次测验成绩(单位:分),如图是两人赛前5次测验成绩的折线统计图.
为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛,统计了他们从今年1到5月的每个月的一次测验成绩(单位:分),如图是两人赛前5次测验成绩的折线统计图. 如图,点A是半径为2的⊙O与双曲线y=
如图,点A是半径为2的⊙O与双曲线y=