Question

【题目】（1）如图1，四边形ABCD为正方形，BF⊥AE，那么BF与AE相等吗？为什么？

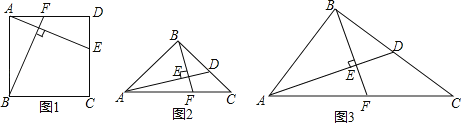
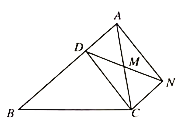
（2）如图2，在Rt△ABC中，BA＝BC，∠ABC＝90°，D为BC边的中点，BE⊥AD于点E，交AC于F，求AF：FC的值；

（3）如图3，Rt△ACB中，∠ABC＝90°，D为BC边的中点，BE⊥AD于点E，交AC于F，若AB＝3，BC＝4，求CF．

Answer 1

【答案】（1）BF=AE，理由见详解 （2）AF：FC=2：1 （3）CF=．

【解析】

(1)先判断出AB=AD，再利用同角的余角相等，判断出∠ABF=∠DAE，进而得出△ABF△DAE，即可得出结论；

（2）构造出正方形，同（1）的方法得出△ABD≌△CBG，进而得出CG=AB，再判断出△AFB∽△CFG，即可得出结论；

（3）先构造出矩形，同（1）的方法得，∠BAD=∠CBP，进而判断出△ABD∽△BCP，即可求出CP，再同（2）的方法判断出△CFP∽△AFB,建立方程即可得出结论．

解：（1）BF=AE，理由：

∵四边形ABCD是正方形，

∴AB=AD，∠BAD=∠D=90°，

∴∠BAE+∠DAE=90°；

∵AE⊥BF，

∴∠BAE+∠ABF=90°，

∴∠ABF=∠DAE；

在△ABF和△DAE中,

，

∴△ABF△DAE，

∴BF=AE．

(2)如图2：

过点A作AM‖BC, 过点C作CM‖AB,两线相较于M，延长BF交CM于G，

∴四边形ABCM是平行四边形，

∵∠ABC=90°，

∴平行四边形ABCM是矩形，

∵AB=BC，

∴矩形ABCM是正方形，

∴AB=BC=CM；

同（1）的方法得，△ABD△CBG，

∴CG=BD；

又∵D为BC边的中点，

∴BD=BC=CM，

∴CG=CMAB；

∵AB‖CM，

∴△AFB△CFG，

∴==2．

(3)如图3：

在Rt△ACB中，AB＝3，BC＝4，

∴AC=5，

∵点D是BC的中点，

∴BD=BC=2；

过点A作AN‖BC, 过点C作CN∥AB,两线相较于N，延长BF交CN于P，

∴四边形ABCN是平行四边形，

∵∠ABC=90°，

∴平行四边形ABCN是矩形，

同（1）的方法得，∠BAD=∠CBP，

∵∠ABD=∠BCP=90°，

∴△ABD△BCP，

∴=，

∴=，

∴CP=；

同（2）的方法得：△CFP△AFB,

∴=，

∴=，

∴CF=．