Question

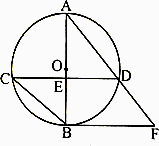
如下图，⊙O的直径AB为10 cm，弦AC为6 cm，∠ACB的平分线交AB于E，交⊙O于D．求弦AD、CD的长．

Answer 1

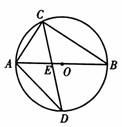
解：∵ AB是直径，∴ ∠ACB = 90°．

在Rt△ABC中，BC == 8（cm）．

∵ CD平分∠ACB， ∴ =，进而AD = BD．

于是在Rt△ABD中，得 AD = BD =AB = 5（cm）．

过E作EF⊥AC于F，EG⊥BC于G，F、G是垂足，则四边形CFEG是正方形．

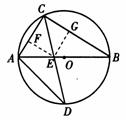
设EF = EG = x，由三角形面积公式，得 AC ? x +BC ? x =AC ? BC，

即 ×6 ? x + 12×8×x = 12×6×8，解得 x =．

∴ CE = 2x =．

由 △ADE∽△CBE，得  DE : BE = AE : CE = AD : BC，

即 DE : BE = AE := 5: 8，

解得 AE =，BE = AB－AE = 10－=， ∴ DE =．

因此 CD = CE + DE =+= 7（cm）．

答：AD、CD的长依次为5cm，7cm．

说明：另法一   求CD时还可以作CG⊥AE，垂足为G，连接OD．

另法二   过A作AF⊥CD于F，则△ACF是等腰直角三角形．