题目内容
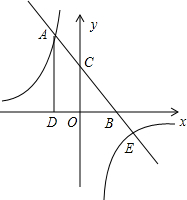 如图,反比例函数y=
如图,反比例函数y= (m≠0)的图象过点E(2,-6),一次函数y=kx+b(k≠0)的图象分别与x轴、y轴交于点B、C,与y=
(m≠0)的图象过点E(2,-6),一次函数y=kx+b(k≠0)的图象分别与x轴、y轴交于点B、C,与y= 的图象在第二象限交于点A,过点A作AD⊥OX,垂足为D,且OB=OD=
的图象在第二象限交于点A,过点A作AD⊥OX,垂足为D,且OB=OD= OC.求反比例函数及一次函数的解析式.
OC.求反比例函数及一次函数的解析式.
解:∵点E(2,-6)在y= 上
上
∴-6= ,
,
∴m=-12(3分)
设B(a,0),由OD=OB= OC知,
OC知,
D(-a,0),C(0,2a)(4分)
∵AD⊥Ox
∴CO∥AD
∴AD=2OC,
∴AD=4a即A(-a,4a)
又A在y= 上
上
∴4a= ,
,
∴a2=3,
∴a=± ,(负值舍去)(7分)
,(负值舍去)(7分)
∴B( ,0),C(0,2),
,0),C(0,2),
又∵B、C在y=kx+b上,
∴O= k+b,2=b
k+b,2=b
∴k=- ,b=2,
,b=2,
∴所求一次函数的解析式为:y=- x+2.(9分)
x+2.(9分)
故答案为:y= 、y=-
、y=- x+2.
x+2.
分析:将E(2,-6)代入y= ,求出m的值,即可求出反比例函数解析式;设B点坐标为(a,0),由OD=OC=OB,AD⊥Ox可用a分别表示出A、D、C三点的坐标,由A在反比例函数的图象上可求出a的值,进而求出各点坐标,把B、C两点的坐标代入一次函数y=kx+b即可求出此函数的表达式.
,求出m的值,即可求出反比例函数解析式;设B点坐标为(a,0),由OD=OC=OB,AD⊥Ox可用a分别表示出A、D、C三点的坐标,由A在反比例函数的图象上可求出a的值,进而求出各点坐标,把B、C两点的坐标代入一次函数y=kx+b即可求出此函数的表达式.
点评:本题考查的是反比例函数与一次函数的交点问题,先用待定系数法求出反比例函数的解析式,再由已知条件分别设出A、B、C、D各点的坐标是解答此题的关键.
 上
上∴-6=
 ,
,∴m=-12(3分)
设B(a,0),由OD=OB=
 OC知,
OC知,D(-a,0),C(0,2a)(4分)
∵AD⊥Ox
∴CO∥AD
∴AD=2OC,
∴AD=4a即A(-a,4a)
又A在y=
 上
上∴4a=
 ,
,∴a2=3,
∴a=±
 ,(负值舍去)(7分)
,(负值舍去)(7分)∴B(
 ,0),C(0,2),
,0),C(0,2),又∵B、C在y=kx+b上,
∴O=
 k+b,2=b
k+b,2=b∴k=-
 ,b=2,
,b=2,∴所求一次函数的解析式为:y=-
 x+2.(9分)
x+2.(9分)故答案为:y=
 、y=-
、y=- x+2.
x+2.分析:将E(2,-6)代入y=
 ,求出m的值,即可求出反比例函数解析式;设B点坐标为(a,0),由OD=OC=OB,AD⊥Ox可用a分别表示出A、D、C三点的坐标,由A在反比例函数的图象上可求出a的值,进而求出各点坐标,把B、C两点的坐标代入一次函数y=kx+b即可求出此函数的表达式.
,求出m的值,即可求出反比例函数解析式;设B点坐标为(a,0),由OD=OC=OB,AD⊥Ox可用a分别表示出A、D、C三点的坐标,由A在反比例函数的图象上可求出a的值,进而求出各点坐标,把B、C两点的坐标代入一次函数y=kx+b即可求出此函数的表达式.点评:本题考查的是反比例函数与一次函数的交点问题,先用待定系数法求出反比例函数的解析式,再由已知条件分别设出A、B、C、D各点的坐标是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y= 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数