题目内容
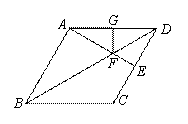
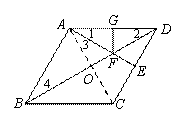
如图,在菱形ABCD中,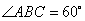 ,过点A作AE⊥CD于点E,交对角线BD于点F,过点F作FG⊥AD于点G.
,过点A作AE⊥CD于点E,交对角线BD于点F,过点F作FG⊥AD于点G.
(1)求证:BF= AE +FG;
(2)若AB=2,求四边形ABFG的面积.
 |
(1)证明: 连结AC,交BD于点O.
∵ 四边形ABCD是菱形,
∴AB= AD,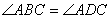 ,∠4=
,∠4=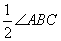 ,
,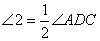 , AC⊥BD ,
, AC⊥BD ,
 ∵
∵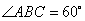 ,
,
∴∠2=∠4=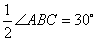 ,
,
又∵AE⊥CD于点E,
∴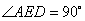 ,
,
∴∠1=30°,
∴∠1=∠4,∠AOB=∠DEA=90°,
∴△ABO≌△DAE,
∴ AE=BO.
 又∵FG⊥AD于点G,
又∵FG⊥AD于点G,
∴∠AOF=∠AGF=90°,
又∵∠1=∠3,AF= AF,
∴△AOF≌△AGF,
∴ FG=FO.
∴BF= AE +FG.
(2)解:∵∠1=∠2=30°,
∴ AF=DF.
又∵FG⊥AD于点G,
∴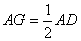 ,
,
∵AB=2,
∴AD=2,AG=1.
∴DG=1,AO=1,FG=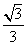 ,BD=
,BD=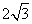 ,
,
∴△ABD的面积是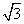 ,RT△DFG的面积是
,RT△DFG的面积是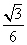
∴四边形ABFG的面积是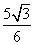 .
.
(注:其它证法请对应给分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某路段的雷达测速器对一段时间内通过的汽车进行测速,将监测到的数据加以整理,得到下面不完整的图表:
| 时速段 | 频数 | 频率 |
| 30~40 | 10 | 0.05 |
| 40~50 | 36 | 0.18 |
| 50~60 | 0.39 | |
| 60~70 | ||
| 70~80 | 20 | 0.10 |
| 总 计 | 200 | 1 |
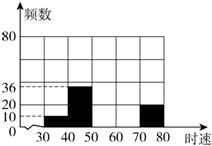
注:30~40为时速大于或等于30千米且小于40千米,其它类同.
(1) 请你把表中的数据填写完整;
(2) 补全频数分布直方图;
(3) 如果此路段汽车时速达到或超过60千米即为违章,那么违章车辆共有多少辆?
 =AC,∠A=36°,DE垂直平分AB,△BEC的周长为20,BC=9。
=AC,∠A=36°,DE垂直平分AB,△BEC的周长为20,BC=9。
 ,CF⊥AD于点E,
,CF⊥AD于点E,
 =-4
=-4 C. m<0 D.0<m<
C. m<0 D.0<m< 有一个实数解x=1,则m的取值是( )
有一个实数解x=1,则m的取值是( )
